题目内容
已知实数x、y满足2x+y=8，当2≤x≤3时，求
的最大值与最小值.
【探究】 为了利用斜率，应作恒等变形
，即过原点的直线OP的斜率
，其中(x,y)为点P的坐标.
【解析】如图所示，由于点(x,y)满足关系式2x+y=8,且2≤x≤3,可知点P在线段AB上移动，并且A、B两点的坐标可分别求得为A(2，4)，B(3，2).
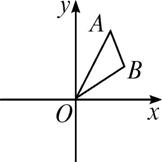
由于
的几何意义是直线OP的斜率，且kOA=2,KOB=
,
所以可以得
的最大值为2，最小值为
.
【规律总结】 利用斜率公式解决代数问题的关键是：根据代数式的结构进行联想，看是否能写成
的形式.
练习册系列答案
相关题目
已知实数x，y满足x2+y2-4x+6y+12=0，则|2x-y-2|的最小值是（ ）
A、5-
| ||
B、4-
| ||
| C、5 | ||
| D、4 |