题目内容
设斜率为2 的直线
的直线 过抛物线
过抛物线 的焦点F,且和
的焦点F,且和 轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )
轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )
A. | B. | C. | D. |
B
解析

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
顶点在原点,且过点 的抛物线的标准方程是( )
的抛物线的标准方程是( )
A. | B. |
C. 或 或 | D. 或 或 |
若点 的坐标是
的坐标是 ,F是抛物线
,F是抛物线 的焦点,点
的焦点,点 在抛物线上移动,为使得
在抛物线上移动,为使得 取得最小值,则
取得最小值,则 点的坐标是
点的坐标是 ( )
( )
A. | B. | C. | D.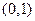 |
已知两点 和
和 ,若曲线上存在点P,使
,若曲线上存在点P,使 ,则称该曲线为“Q型曲线”. 给出下列曲线:①
,则称该曲线为“Q型曲线”. 给出下列曲线:① ;②
;② ;③
;③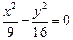 ;④
;④ ,其中为“Q型曲线”的是 ( )
,其中为“Q型曲线”的是 ( )
| A.①和② | B.②和③ | C.①和④ | D.②和④ |
若双曲线 的左右焦点分别为
的左右焦点分别为 、
、 ,线段
,线段
被抛物线 的焦点分成
的焦点分成 的两段,则此双曲线的离心率为( )
的两段,则此双曲线的离心率为( )
A. | B.  | C. | D. |
抛物线 的准线方程是 ( )
的准线方程是 ( )
A. | B. | C. | D. |
双曲线 的两条渐近线和直线x=2围成一个三角形区域(含边界),则该区域可表示为
的两条渐近线和直线x=2围成一个三角形区域(含边界),则该区域可表示为
A. | B. | C. | D. |
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,抛物线
,抛物线 的
的 的左准线重合,若双曲线
的左准线重合,若双曲线 满
满 ,则双曲线
,则双曲线 分别是双曲线
分别是双曲线 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则 的取值范围为 ( )
的取值范围为 ( )


