题目内容
17.在△ABC中,角A,B,C所对应的边分别为a,b,c,a-b=bcosC.(1)求证:sinC=tanB
(2)若a=2,b=2,求c.
分析 (1)根据正弦定理和三角形内角和定理,利用和与差打开即可得证.
(2)根据a-b=bcosC,a=2,b=2,求出cosC,利用余弦定理可得解.
解答 解:(1)由题意,a-b=bcosC,
根据正弦定理得:sinA-sinB=sinBcosC.
即sin(B+C)-sinB=sinBcosC.
sinBcosC+sinCcosB-sinB=sinBcosC.
得:sinCcosB=sinB
可得sinC=tanB.
(2)由a-b=bcosC,a=2,b=2,
得cosC=0.即C=90°
由余弦定理,c2=a2+b2-2abcosC.
得:c2=8.
∴c=2$\sqrt{2}$.
点评 本题考查了正余弦定理和三角形内角和定理,和与差公式的运用.属于基础题.

练习册系列答案
相关题目
5.己知随机变量X服从正态分布N(μ,σ2),且P(μ-2σ<X≤μ+2σ)=0.9545,P(μ-σ<X≤μ+σ)=0.6827,若μ=3,σ=1,则P(4<X≤5)=( )
| A. | 0.1358 | B. | 0.1359 | C. | 0.2716 | D. | 0.2718 |
12.设全集U=R,集合A={x|-1<x<3},B={x|x<1},则A∩(∁UB)=( )
| A. | {x|1<x<3} | B. | {x|1≤x<3} | C. | {x|1<x≤3} | D. | {x|1≤x≤3} |
2.“a≥-2”是“函数f(x)=x|x+a|在[2,+∞)上单调递增”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.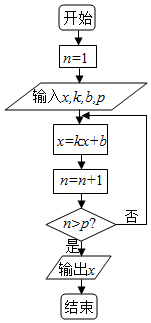 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
 如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别为1,-2,9,3,则输出x的值为( )| A. | -29 | B. | 19 | C. | 47 | D. | -5 |
 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,利用随机模拟方法计算阴影部分面积时,利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=a1+1,b=4b1,试验进行100次,前98次中落在阴影部分内的样本点数为40,且最后两次试验的随机数为a1=0.5,b1=0.3及a1=0.2,b1=0.6,那么本次模拟得出的面积约为1.64.
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,利用随机模拟方法计算阴影部分面积时,利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=a1+1,b=4b1,试验进行100次,前98次中落在阴影部分内的样本点数为40,且最后两次试验的随机数为a1=0.5,b1=0.3及a1=0.2,b1=0.6,那么本次模拟得出的面积约为1.64.