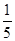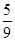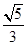题目内容
在△ABC中,设角A、B、C的对边分别为a、b、c,且acosC+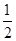 c=b.
c=b.
(1)求角A的大小;
(2)若a=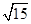 ,b=4,求边c的大小.
,b=4,求边c的大小.
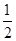 c=b.
c=b.(1)求角A的大小;
(2)若a=
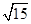 ,b=4,求边c的大小.
,b=4,求边c的大小.(1)A=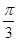 .(2)c=2±
.(2)c=2±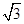
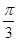 .(2)c=2±
.(2)c=2±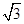
(1)用正弦定理,由acosC+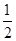 c=b,得sinAcosC+
c=b,得sinAcosC+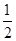 sinC=sinB.
sinC=sinB.
∵sinB=sin(A+C)=sinAcosC+cosAsinC,∴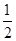 sinC=cosAsinC.
sinC=cosAsinC.
∵sinC≠0,∴cosA=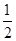 .∵0<A<π,∴A=
.∵0<A<π,∴A=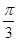 .
.
(2)用余弦定理,得a2=b2+c2-2bccosA.
∵a=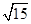 ,b=4,∴15=16+c2-2×4×c×
,b=4,∴15=16+c2-2×4×c×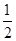
即c2-4c+1=0.则c=2±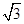 .
.
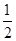 c=b,得sinAcosC+
c=b,得sinAcosC+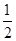 sinC=sinB.
sinC=sinB.∵sinB=sin(A+C)=sinAcosC+cosAsinC,∴
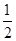 sinC=cosAsinC.
sinC=cosAsinC.∵sinC≠0,∴cosA=
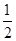 .∵0<A<π,∴A=
.∵0<A<π,∴A=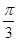 .
.(2)用余弦定理,得a2=b2+c2-2bccosA.
∵a=
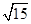 ,b=4,∴15=16+c2-2×4×c×
,b=4,∴15=16+c2-2×4×c×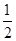
即c2-4c+1=0.则c=2±
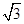 .
.
练习册系列答案
相关题目
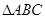 中,角
中,角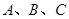 所对的边分别为
所对的边分别为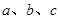 ,
,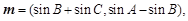
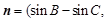
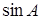 ),且
),且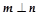 .
.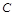 的大小;
的大小;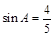 ,求
,求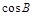 的值.
的值.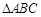 中,内角
中,内角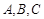 的对边分别为
的对边分别为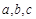 ,且
,且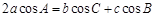 .
.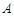 的大小;
的大小;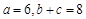 ,求
,求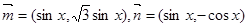 ,设函数
,设函数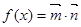 ,若函数
,若函数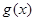 的图象与
的图象与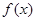 的图象关于坐标原点对称.
的图象关于坐标原点对称.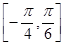 上的最大值,并求出此时
上的最大值,并求出此时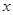 的取值;
的取值;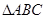 中,
中,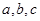 分别是角
分别是角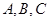 的对边,若
的对边,若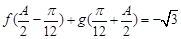 ,
,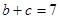 ,
,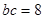 ,求边
,求边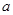 的长.
的长.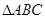 中,角
中,角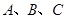 所对的边分别为
所对的边分别为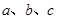 ,已知
,已知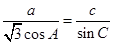 ,
,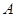 的大小;
的大小;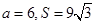 ,求
,求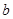 和
和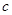 的值.
的值.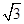 b-c)cosA=acosC,则cosA= .
b-c)cosA=acosC,则cosA= .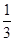 ,则sinB等于( )
,则sinB等于( )