题目内容
过椭圆 +
+ =1(0<b<a)中心的直线与椭圆交于A、B两点,右焦点为F2(c,0),则△ABF2的最大面积是 ( )
=1(0<b<a)中心的直线与椭圆交于A、B两点,右焦点为F2(c,0),则△ABF2的最大面积是 ( )
A.ab B.ac C.bc D.b2
【答案】
C
【解析】主要考查椭圆的定义、几何性质,以及数形结合思想。
设面积为S,点A的纵坐标为 ,由于直线过椭圆中心,故B的纵坐标为-
,由于直线过椭圆中心,故B的纵坐标为-
三角形的面积S= |OF2||
|OF2|| |+
|+ |OF2||-
|OF2||- |=|OF2||
|=|OF2|| |
|
由于|OF2|为定值c,三角形的面积只与 有关,
有关,
又由于| |
| b,显然,当|
b,显然,当| |=b时,三角形的面积取到最大值bc,
|=b时,三角形的面积取到最大值bc,
此时,直线为y轴,故选C。
思路拓展:注重运用数形结合思想,避免繁琐计算。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,椭圆C:
如图,椭圆C: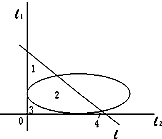 (2010•江西模拟)如图,过椭圆中心的直线l与经椭圆长短轴端点的两条切线l1,l2分别交于点A、B,O是l1与l2的交点,△AOB被椭圆分成四部分,若这四部分图形的面积满足S1+S3=S2+S4,则直线l有( )
(2010•江西模拟)如图,过椭圆中心的直线l与经椭圆长短轴端点的两条切线l1,l2分别交于点A、B,O是l1与l2的交点,△AOB被椭圆分成四部分,若这四部分图形的面积满足S1+S3=S2+S4,则直线l有( )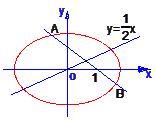
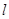 与中心在原点,焦点在x轴上且离心率为
与中心在原点,焦点在x轴上且离心率为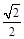 的椭圆C相交于A、B两点,直线y=
的椭圆C相交于A、B两点,直线y=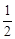 x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l对称,试求直线l与椭圆C的方程
x过线段AB的中点,同时椭圆C上存在一点与其右焦点关于直线l对称,试求直线l与椭圆C的方程