题目内容
设命题p:函数f(x)=x3-ax-1在区间[-1,1]上单调递减;命题q:
函数y=ln(x2+ax+1)的值域是R.如果命题p或q为真命题,p且q为假命题,
求a的取值范围.
解:p为真命题⇔f′(x)=3x2-a≤0在[-1,1]上恒成立
⇔a≥3x2在[-1,1]上恒成立⇔a≥3. ……………3分
q为真命题⇔Δ=a2-4≥0恒成立⇔a≤-2或a≥2. ……………6分
由题意p和q有且只有一个是真命题. …………………………7分
p真q假⇔ ⇔a∈∅, ………………………9分
⇔a∈∅, ………………………9分
p假q真⇔ ⇔a≤-2或2≤a<3. ………………………11分
⇔a≤-2或2≤a<3. ………………………11分
综上可知:a∈(-∞,-2]∪[2,3).………………………12分

练习册系列答案
相关题目
 且
且 成立,当
成立,当 时,有
时,有 ( )
( ) B、
B、 C、
C、 D、
D、
 是椭圆
是椭圆 上的一动点,
上的一动点, 为椭圆的两个焦点,
为椭圆的两个焦点, 是
是 是
是 的角平分线上的一点,且
的角平分线上的一点,且 ,则
,则 的取值范
的取值范 B.
B. C.
C. D.
D.
 则( ).
则( ). B.
B. C.
C. D.
D.
 +2)=x+2
+2)=x+2 的值是( )
的值是( ) B.
B. C.
C. D.
D.
 等于( )
等于( ) B.
B. C.16或9 D.12
C.16或9 D.12 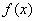 =log2(3x-1)的定义域为( )
=log2(3x-1)的定义域为( ) 属于特征值l的一个特征向量为α=
属于特征值l的一个特征向量为α=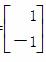 .
.