题目内容
【题目】如图,2012年春节,摄影爱好者![]() 在某公园
在某公园![]() 处,发现正前方
处,发现正前方![]() 处有一立柱,测得立柱顶端
处有一立柱,测得立柱顶端![]() 的仰角和立柱底部
的仰角和立柱底部![]() 的俯角均为
的俯角均为![]() ,设
,设![]() 的眼睛距地面的距离
的眼睛距地面的距离![]() 米.
米.
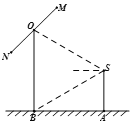
(1)求摄影者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆![]() 绕其中点
绕其中点![]() 在
在![]() 与立柱所在的平面内旋转.摄影者有一视角范围为
与立柱所在的平面内旋转.摄影者有一视角范围为![]() 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
【答案】(1)![]() ,
,![]() ;(2)摄影者可以将彩杆全部摄入画面.
;(2)摄影者可以将彩杆全部摄入画面.
【解析】
试题分析:(1)摄影者眼部记为点![]() ,作
,作![]() 于
于![]() ,则有
,则有![]() ,
,![]() .
.![]() ,在
,在![]() 中,由三角函数的定义可求
中,由三角函数的定义可求![]() ;再由
;再由![]() ,
,![]() ,在
,在![]() 中由三角函数的定义可求
中由三角函数的定义可求![]() ,进而可求
,进而可求![]() ;(2)以
;(2)以![]() 为原点,以水平方向向右为
为原点,以水平方向向右为![]() 轴正方向建立平面直角坐标系.设
轴正方向建立平面直角坐标系.设![]() ,
,![]() ,则
,则![]() ,由(1)知
,由(1)知![]() ,利用向量的数量积的坐标表示可求
,利用向量的数量积的坐标表示可求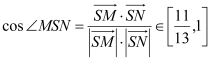 ,结合余弦函数的性质可求答案.
,结合余弦函数的性质可求答案.
试题解析:(1)作![]() 垂直
垂直![]() 于
于![]() ,则
,则![]() ,
,![]() .
.
又![]() ,故在
,故在![]() 中,可求得
中,可求得![]() ,即摄影者到立柱的水平距离为
,即摄影者到立柱的水平距离为![]() 米.
米.
由![]() ,
,![]() ,在
,在![]() 中,可求得
中,可求得![]() .
.
因为![]() ,故
,故![]() ,即立柱高为
,即立柱高为![]() 米.
米.
(2)如图,![]() 为原点,以水平方向向右为
为原点,以水平方向向右为![]() 轴正方向建立平面直角坐标系.
轴正方向建立平面直角坐标系.
设![]() ,
,![]() ,则
,则![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() .
.
故![]() ,
,![]() ,
,
∴![]()
![]()
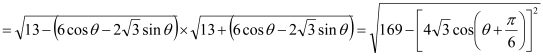

由![]() 知
知![]() 所以
所以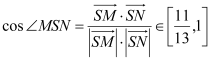 ,
,
∴![]() 恒成立
恒成立
故在彩杆转动的任意时刻,摄影者都可以将彩杆全部摄入画面

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目

