题目内容
20.设函数f(x)=(x2-8x+c1)(x2-8x+c2)(x2-8x+c3)(x2-8x+c4),集合M={x|f(x)=0}={x1,x2,x3,…,x7}⊆N*,设c1≥c2≥c3≥c4则c1-c4=( )| A. | 11 | B. | 13 | C. | 7 | D. | 9 |
分析 由已知中集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,结合函数f(x)的解析式,及韦达定理,我们易求出c1及c4的值,进而得到答案
解答 解:由根与系数的关系知xi+yi=8,xi•yi=ci,
这里xi,yi为方程x2-8x+ci=0之根,i=1,…,4.
又∵M={x|f(x)=0}={x1,x2,…,x7}⊆N*,
由集合性质可得(xi,yi)取(1,7),(2,6),(3,4),(4,4),
又c1≥c2≥c3≥c4,
故c1=16,c4=7
∴c1-c4=9
故选:D
点评 本题考查的知识点是函数与方程的综合运用,其中根据韦达定理,求出c1及c4的值,是解答本题的关键

练习册系列答案
相关题目
10.执行如图所示的程序框图,若输出的S=183,则判断框内应填入的条件是( )
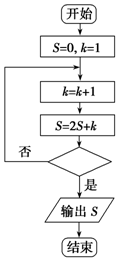

| A. | k>7? | B. | k>6? | C. | k>5? | D. | k>4? |
9.已知圆 C1:x2+y2+2x+3y+1=0,圆 C2:x2+y2+4x+3y+2=0,圆C1与圆C2的位置关系为( )
| A. | 外切 | B. | 相离 | C. | 相交 | D. | 内切 |