题目内容
在直角梯形ABCD中,∠D=∠BAD=90°,AD=DC= AB=1,将△ADC 沿AC折起,使D到D′.若二面角D′-AC-B为60°,则三棱锥D′-ABC的体积为________.
AB=1,将△ADC 沿AC折起,使D到D′.若二面角D′-AC-B为60°,则三棱锥D′-ABC的体积为________.
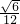
分析:欲求三棱锥D′-ABC的体积,只需找到它的底面与高,因为三角形ABC的面积易求,所以只需求出D′到平面ABC的距离即可,由(1)可知,即求线段D′E的长度,可放入三角形中,通过解三角形得到,这样,三棱锥体积可求.
解答:
 解:设面ACD′为α,面ABC为β,取AC的中点E,连接D′E,再过D′作D′O⊥β,垂足为O,连接OE,则D′E⊥AC
解:设面ACD′为α,面ABC为β,取AC的中点E,连接D′E,再过D′作D′O⊥β,垂足为O,连接OE,则D′E⊥AC∵AC⊥D′E,∴AC⊥OE
∴∠D′EO为二面角a-AC-β的平面角,∴∠D′EO=60°
在直角梯形ABCD中,由已知△DAC为等腰直角三角形,
∴AC=
 ,∠CAB=45°,∴D′E=
,∠CAB=45°,∴D′E= AC=
AC= ,
,在直角△D′OE中,D′E=
 ,∴D′O=
,∴D′O=
∴VD-ABC=
 S△ABC•D′O=
S△ABC•D′O= ×
× AC•BC•D′O=
AC•BC•D′O= ×
× ×
× ×
× =
=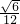 .
.故答案为:
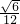
点评:本题考查了二面角的求法,以及三棱锥体积的求法,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
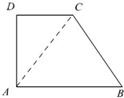
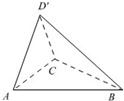
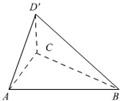
 (2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
(2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
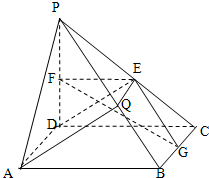
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD= 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为