题目内容
已知x∈R,求证:ex≥x+1.
答案:
解析:
提示:
解析:
|
解:令f(x)=ex-x-1,则 当x∈[0,+∞)时,∵ex-1≥0, ∴f(x)在[0,+∞)上是增函数,这时f(x)≥f(0)=0. 当x∈(-∞,0)时, ∵ex-1<0, ∴f(x)在(-∞,0)上是减函数,这时f(x)>f(0)=0. 综上,当x∈R时,f(x)≥0,即ex≥x+1. 解析:构造函数f(x)=ex-x-1,利用导数符号判断f(x)的单调性,求出最小值M,证明f(x)≥M≥0. |
提示:
|
根据导数的符号证明原函数的单调性是处理与单调性有关的问题时一种比较简便的方法. |

练习册系列答案
相关题目
 附加题:
附加题:
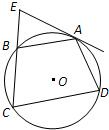
 A.如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,DE交AB于点F.求证:△PDF∽△POC.
A.如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,DE交AB于点F.求证:△PDF∽△POC.