题目内容
函数y=sin(πx+
)(＞0)的部分图象如图所示，设P是图像的最高点，A，B是图像与x轴的交点，记∠APB=θ，则sin2θ的值是( )
A． | B． | C．－ | D．－ |
A
解析试题分析：由周期公式可知函数周期为2，∴AB=2，过P作PD⊥AB与D，根据周期的大小看出直角三角形中直角边的长度，解出∠APD与∠BPD的正弦和余弦，利用两角和与差公式求出sinθ，进而求得sin2θ．
考点：（1）三角函数的性质；（2）解三角形.
练习册系列答案
相关题目
函数
的图象的一条对称轴的方程是( )
A． | B． | C． | D． |
若
，则计算
所得的结果为（ ）
A． | B． | C． | D． |
的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象向左平移
个单位，得到的图象对应的解析式是（ ）
函数
是（ ）
A．最小正周期为 的奇函数 | B．最小正周期为的偶函数 |
C．最小正周期为 的奇函数 | D．最小正周期为的偶函数 |
函数
的部分图象如图所示，为了得到
的图象，只需将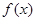
的图象( )
A．向右平移 个单位 | B．向右平移 个单位 |
| C．向左平移个单位 | D．向左平移个单位 |
已知函数f(x)=2sin(ωx+
),x∈R,其中ω>0,-π<≤π.若f(x)的最小正周期为6π,且当x=
时,f(x)取得最大值,则( )
| A．f(x)在区间[-2π,0]上是增函数 |
| B．f(x)在区间[-3π,-π]上是增函数 |
| C．f(x)在区间[3π,5π]上是减函数 |
| D．f(x)在区间[4π,6π]上是减函数 |
,则函数g(x)=asinx+cosx的最大值是( )
函数y=cos(2x+
)的图象的一条对称轴方程是( )
| A．x=- | B．x=- |
C．x= | D．x=π |