题目内容
已知数列 各项均为正数,满足
各项均为正数,满足 .
.
(1)计算 ,并求数列
,并求数列 的通项公式;
的通项公式;
(2)求数列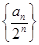 的前
的前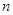 项和
项和 .
.
(1) ,
, ,
, ;(2)
;(2) .
.
解析试题分析:(1)将已知条件因式分解 , 因为数列
, 因为数列 各项均为正数,所以
各项均为正数,所以 ,将
,将 代入可得
代入可得 ,将
,将 代入可得
代入可得 ;(2)由(1)知
;(2)由(1)知 为等差数列,而
为等差数列,而 为等比数列,故求数列
为等比数列,故求数列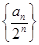 的前
的前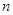 项和
项和 时利用错位相减法.
时利用错位相减法.
试题解析:(1)∵ 


又 ∵ 数列 各项均为正数 ∴
各项均为正数 ∴  ,故
,故
 .
.
(2)

∴ .
.
考点:等差数列、错位相减法求数列的和.

练习册系列答案
相关题目
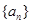 满足:
满足: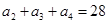 ,且
,且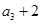 是
是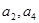 的等差中项.
的等差中项.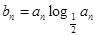 ,
,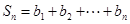 ,求使
,求使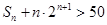 成立的正整数
成立的正整数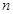 的最小值.
的最小值.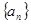 的前
的前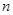 项的和为
项的和为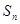 ,点
,点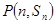
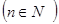 在函数
在函数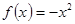
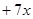 的图象上.
的图象上.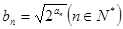 ,求数列
,求数列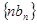 的前
的前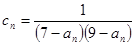 ,数列
,数列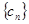 的前
的前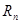 ,求使不等式
,求使不等式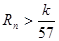 对一切
对一切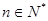 都成立的最大正整数
都成立的最大正整数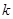 的值.
的值.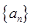 的前
的前 项和为
项和为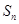 ,
,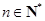 ,且
,且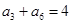 ,
,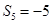 .
.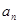 ;
; ,求
,求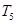 的值和
的值和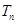 的表达式.
的表达式.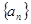 满足
满足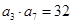 ,
,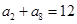 ,且
,且 (
(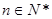 ).
).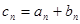 ,求数列
,求数列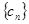 的前n项和
的前n项和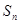 .
.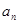 }中,
}中,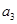 =3,前7项和
=3,前7项和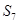 =28。
=28。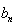 }为等比数列,且
}为等比数列,且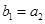 ,
,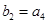 求数列
求数列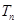
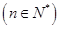 .
.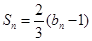 且
且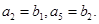
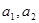 是方程x2-14x+45=0的两根,求数列
是方程x2-14x+45=0的两根,求数列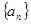 通项公式(2)设
通项公式(2)设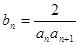 ,数列{bn}的前n项和为Sn,证明
,数列{bn}的前n项和为Sn,证明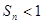 .
.