题目内容
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.(Ⅰ)证明:AB1⊥BC1;
(Ⅱ)求二面角C-AC1-B的大小;
(Ⅲ)求点B到平面AB1Cl的距离.
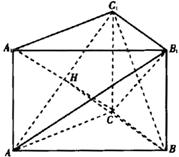
解法一:(Ⅰ)在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC,所以CC1⊥AC,

因为BC=CC1,所以BCC1B1为正方形,
又∠ACB=90°,所以AC⊥BC,
所以AC⊥平面BCC1B1,
连结B1C,则B1C为AB1在平面BCC1B1上的射影,
因为B1C⊥BC1,所以AB1⊥BC1.
(Ⅱ)连A1C交AC1于点H,连BH,因为BC⊥AC,
BC⊥CC1,BC⊥平面ACC1A1,
所以CH为BH在平面ACC1A1上的射影,
因为四边形ACC1A1为正力形,所以CH⊥AC1,所以BH⊥AC1,
所以,∠CHB为二面角C-AC1-D的平面角.
在直角△BCH中,CH=![]() ,BC=2,所以tan∠CHB=
,BC=2,所以tan∠CHB=![]() ,
,
所以,二面角C-AC1-B的大小为arctan![]() .
.
(Ⅲ)因为BC∥B1C1,BC![]() 面AB1C1,所以BC∥面AB1C1,所以点B到平面AB1C1的距离等于点C到平面AB1C1的距离.
面AB1C1,所以BC∥面AB1C1,所以点B到平面AB1C1的距离等于点C到平面AB1C1的距离.
因为BC⊥CH,所以B1C1⊥CH,
又CH⊥AC1,所以CH⊥平面AB1C1,
所以CH的长度为点置到平面AB1C1的距离,
CH=![]() A1C=
A1C=![]() .
.
解法二:(Ⅰ)如图建立直角坐标系,其中C为坐标原点.
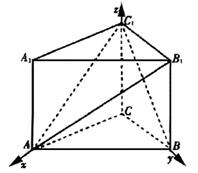
依题意A(2,0,0),B(0,2,0),B1(0,2,2),C1(0,0,2)(2分)
因为![]() =(-2,2,2)·(0,-2,2)=0,
=(-2,2,2)·(0,-2,2)=0,
所以AB1⊥BC1(4分)
(Ⅱ)因为BC⊥AC,BC⊥CC1,所以![]() 为平面ACC1的法向量,
为平面ACC1的法向量,![]() =(0,2,0),(5分)
=(0,2,0),(5分)
设n1=(xl,y1,z1)是平面ABC1的法向量,
由n1·![]() =0,n1·
=0,n1·![]() =0,得
=0,得
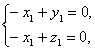 所以
所以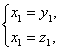
令z1=1,则n1=(1,1,1),
因为cos<![]() ,n1>=
,n1>=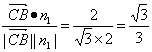 ,
,
所以,二面角C-AC1-B的大小为arocos![]() .
.
(Ⅲ)设n2=(x2,y2,z2)是平面AB1C1的法向量,
由n2·![]() =0,n2·
=0,n2·![]() =0,得
=0,得
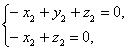 所以
所以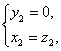
令z2=l,则n2=(1,0,1),(11分)
因为![]() =(-2,2,0),所以,B到平面AB1C1的距离为d=
=(-2,2,0),所以,B到平面AB1C1的距离为d=![]() .
.





