题目内容
(2011•朝阳区三模)已知函数f(x)=
sin2x+sinxcosx-
(x∈R).
(Ⅰ)求f(
)的值;
(Ⅱ)若x∈(0,
),求f(x)的最大值.
| 3 |
| ||
| 2 |
(Ⅰ)求f(
| π |
| 4 |
(Ⅱ)若x∈(0,
| π |
| 2 |
分析:(Ⅰ)直接利用函数的表达式,求解f(
)的值;
(Ⅱ)利用二倍角公式,两角差的正弦函数,化简函数的表达式,通过x∈(0,
),结合三角函数的有界性直接求出函数f(x)的最大值.
| π |
| 4 |
(Ⅱ)利用二倍角公式,两角差的正弦函数,化简函数的表达式,通过x∈(0,
| π |
| 2 |
解答:(本小题满分13分)
解:(Ⅰ)f(
)=
sin2
+sin
cos
-
=
. …(4分)
(Ⅱ)f(x)=
+
sin2x-
=
sin2x-
cos2x=sin(2x-
). …(6分)
∵0<x<
,
∴-
<2x-
<
.
∴当2x-
=
时,即x=
时,f(x)的最大值为1. …(8分)
解:(Ⅰ)f(
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
(Ⅱ)f(x)=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∵0<x<
| π |
| 2 |
∴-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴当2x-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
点评:本题考查三角函数的化简求值,二倍角公式与两角差的三角函数的应用,三角函数的有界性的应用,考查计算能力.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 (2011•朝阳区三模)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
(2011•朝阳区三模)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=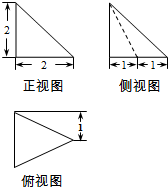 (2011•朝阳区三模)一空间几何体的三视图如图所示,则该几何体的体积为( )
(2011•朝阳区三模)一空间几何体的三视图如图所示,则该几何体的体积为( ) (2011•朝阳区三模)右图是一个几何体的三视图(单位:cm),根据图中数据,可得该几何体的体积是
(2011•朝阳区三模)右图是一个几何体的三视图(单位:cm),根据图中数据,可得该几何体的体积是