题目内容
15.设等差数列{an}的前n项和为Sn,已知S3=15,S9=153,则S6=66.分析 直接由已知结合S3,S6-S3,S9-S6仍为等差数列列式求得S6的值.
解答 解:在等差数列{an}中,
由S3,S6-S3,S9-S6仍为等差数列,得
2(S6-15)=15+(153-S6),
解得:S6=66.
故答案为:66.
点评 本题考查了等差数列的性质,是基础的计算题.

练习册系列答案
相关题目
6. 如图,已知直线l⊥平面α,垂足为O,在△ABC中,BC=2,AC=2,AB=2$\sqrt{2}$,点P是边AC的中点.该三角形在空间按以下条件作自由移动:
如图,已知直线l⊥平面α,垂足为O,在△ABC中,BC=2,AC=2,AB=2$\sqrt{2}$,点P是边AC的中点.该三角形在空间按以下条件作自由移动:
(1)A∈l,(2)C∈α.则|$\overrightarrow{OP}$+$\overrightarrow{PB}$|的最大值为( )
 如图,已知直线l⊥平面α,垂足为O,在△ABC中,BC=2,AC=2,AB=2$\sqrt{2}$,点P是边AC的中点.该三角形在空间按以下条件作自由移动:
如图,已知直线l⊥平面α,垂足为O,在△ABC中,BC=2,AC=2,AB=2$\sqrt{2}$,点P是边AC的中点.该三角形在空间按以下条件作自由移动:(1)A∈l,(2)C∈α.则|$\overrightarrow{OP}$+$\overrightarrow{PB}$|的最大值为( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 1+$\sqrt{5}$ | D. | $\sqrt{10}$ |
3.设数列{an}的前n项和为Sn,若an+Sn=1,则a4=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{64}$ |
10.设i为虚数单位,则复数i2015等于( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
4.已知集合A={x|x2-2x>0},B={x|log2(x+1)<1},则A∩B等于( )
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,1) | D. | (-1,0) |
5.已知点O为双曲线C的对称中心,过点O的两条直线l1与l2的夹角为60°,直线l1与双曲线C相交于点A1,B1,直线l2与双曲线C相交于点A2,B2,若使|A1B1|=|A2B2|成立的直线l1与l2有且只有一对,则双曲线C离心率的取值范围是( )
| A. | ($\frac{2\sqrt{3}}{3}$,2] | B. | [$\frac{2\sqrt{3}}{3}$,2) | C. | ($\frac{2\sqrt{3}}{3}$,+∞) | D. | [$\frac{2\sqrt{3}}{3}$,+∞) |
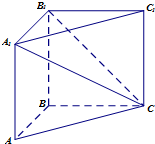 如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.
如图所示:在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=BB1,则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$.