题目内容

F为双曲线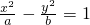： $数学公式$ 左焦点，过其上一点 P作直线PF⊥x轴，交双曲线于p，若PF等于焦距，求双曲线的离心率________．

$\text{[math]}$
分析：先确定双曲线的左焦点坐标，进而可求PF的长，利用|PF|等于焦距，PF⊥x轴，即可求得双曲线的离心率
解答：由题意，设F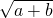（- $\text{[math]}$ ，0），代入双曲线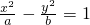： $\text{[math]}$ 可得 $\text{[math]}$
∴ $\text{[math]}$
∵|PF|等于焦距，PF⊥x轴
∴ $\text{[math]}$
∵ $\text{[math]}$
∴ $\text{[math]}$
∴c⁴-6ac²+a²=0
∵ $\text{[math]}$
∴e⁴-6e²+1=0
∵e＞1
∴ $\text{[math]}$
∴e= $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题以双曲线方程为载体，考查双曲线的几何性质，解题的关键是确定几何量之间的关系．

练习册系列答案

黄冈小状元满分冲刺微测验系列答案

新辅教导学系列答案

初中自主学习课时集训系列答案

阳光同学一线名师全优好卷系列答案

过关冲刺100分系列答案

圆梦图书课时达标100分系列答案

高效作业系列答案

倍速学习法系列答案

初中新学案优化与提高系列答案

一遍过系列答案

相关题目

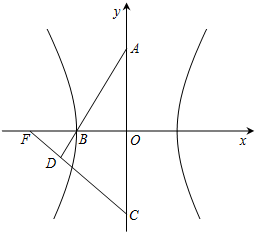如图，双曲线的中心在坐标原点O，A，C分别是双曲线虚轴的上、下顶点，B是双曲线的左顶点，F为双曲线的左焦点，直线AB与FC相交于点D．若双曲线的离心率为2，则∠BDF的余弦值是（　　）

若P为双曲线

=1右支上一个动点，F为双曲线的左焦点，M为PF的中点，O为坐标原点，则|OM|的取值范围为（　　）

F为双曲线：

左焦点，过其上一点 P作直线PF⊥x轴，交双曲线于p，若PF等于焦距，求双曲线的离心率．

如图，双曲线的中心在坐标原点O，A，C分别是双曲线虚轴的上、下顶点，B是双曲线的左顶点，F为双曲线的左焦点，直线AB与FC相交于点D．若双曲线的离心率为2，则∠BDF的余弦值是（）

如图，双曲线的中心在坐标原点O，A，C分别是双曲线虚轴的上、下顶点，B是双曲线的左顶点，F为双曲线的左焦点，直线AB与FC相交于点D．若双曲线的离心率为2，则∠BDF的余弦值是（）