题目内容
已知椭圆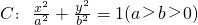 的离心率为
的离心率为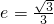 ,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点.
,以原点为圆心,椭圆短半轴长为半径的圆与直线x-y+2=0相切,A,B分别是椭圆的左右两个顶点,P为椭圆C上的动点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若P与A,B均不重合,设直线PA与PB的斜率分别为k1,k2,证明:k1•k2为定值;
(Ⅲ)M为过P且垂直于x轴的直线上的点,若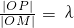 ,求点M的轨迹方程,并说明轨迹是什么曲线.
,求点M的轨迹方程,并说明轨迹是什么曲线.
解:(Ⅰ)由题意可得圆的方程为x2+y2=b2,
∵直线x-y+2=0与圆相切,
∴ ,
,
即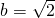 ,
,
又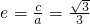 ,
,
即 ,
,
a2=b2+c2,
解得 ,c=1,
,c=1,
所以椭圆方程为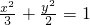 .
.
(Ⅱ)设P(x0,y0)(y0≠0),
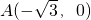 ,
,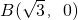 ,
,
则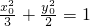 ,即
,即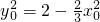 ,
,
则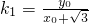 ,
,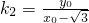 ,
,
即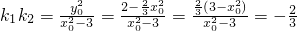 ,
,
∴k1•k2为定值 .
.
(Ⅲ)设M(x,y),其中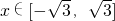 .
.
由已知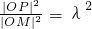 及点P在椭圆C上可得
及点P在椭圆C上可得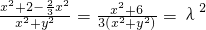 ,
,
整理得(3λ2-1)x2+3λ2y2=6,其中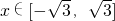 .
.
①当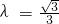 时,化简得y2=6,
时,化简得y2=6,
所以点M的轨迹方程为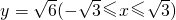 ,轨迹是两条平行于x轴的线段;
,轨迹是两条平行于x轴的线段;
②当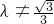 时,方程变形为
时,方程变形为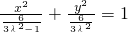 ,其中
,其中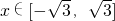 ,
,
当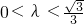 时,点M的轨迹为中心在原点、实轴在y轴上的双曲线满足
时,点M的轨迹为中心在原点、实轴在y轴上的双曲线满足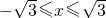 的部分;
的部分;
当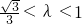 时,点M的轨迹为中心在原点、长轴在x轴上的椭圆满足
时,点M的轨迹为中心在原点、长轴在x轴上的椭圆满足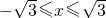 的部分;
的部分;
当λ≥1时,点M的轨迹为中心在原点、长轴在x轴上的椭圆
分析:(I)写出圆的方程,利用直线与圆相切的充要条件列出方程求出b的值,利用椭圆的离心率公式得到a,c的关系,再利用椭圆本身三个参数的关系求出a,c的值,将a,b的值代入椭圆的方程即可.
(II)设出P的坐标,将其代入椭圆的方程得到P的坐标的关系,写出A,B的坐标,利用两点连线的斜率公式求出
k1,k2,将P的坐标的关系代入k1k2化简求出其值.
(III)设出M的坐标,求出P的坐标,利用两点的距离公式将已知的几何条件用坐标表示,通过对参数λ的讨论,判断出M的轨迹.
点评:求圆锥曲线的方程,一般利用待定系数法;解决直线与圆锥曲线的位置关系问题,一般设出直线方程,将直线方程与圆锥曲线方程联立,消去一个未知数,得到关于一个未知数的二次方程,利用韦达定理,找突破口.注意设直线方程时,一定要讨论直线的斜率是否存在.
∵直线x-y+2=0与圆相切,
∴
 ,
,即
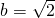 ,
,又
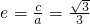 ,
,即
 ,
,a2=b2+c2,
解得
 ,c=1,
,c=1,所以椭圆方程为
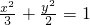 .
.(Ⅱ)设P(x0,y0)(y0≠0),
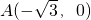 ,
,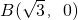 ,
,则
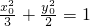 ,即
,即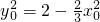 ,
,则
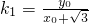 ,
,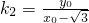 ,
,即
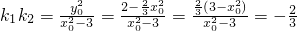 ,
,∴k1•k2为定值
 .
.(Ⅲ)设M(x,y),其中
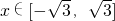 .
.由已知
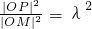 及点P在椭圆C上可得
及点P在椭圆C上可得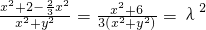 ,
,整理得(3λ2-1)x2+3λ2y2=6,其中
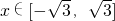 .
.①当
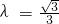 时,化简得y2=6,
时,化简得y2=6,所以点M的轨迹方程为
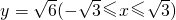 ,轨迹是两条平行于x轴的线段;
,轨迹是两条平行于x轴的线段;②当
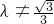 时,方程变形为
时,方程变形为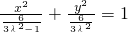 ,其中
,其中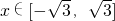 ,
,当
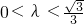 时,点M的轨迹为中心在原点、实轴在y轴上的双曲线满足
时,点M的轨迹为中心在原点、实轴在y轴上的双曲线满足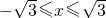 的部分;
的部分;当
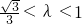 时,点M的轨迹为中心在原点、长轴在x轴上的椭圆满足
时,点M的轨迹为中心在原点、长轴在x轴上的椭圆满足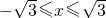 的部分;
的部分;当λ≥1时,点M的轨迹为中心在原点、长轴在x轴上的椭圆
分析:(I)写出圆的方程,利用直线与圆相切的充要条件列出方程求出b的值,利用椭圆的离心率公式得到a,c的关系,再利用椭圆本身三个参数的关系求出a,c的值,将a,b的值代入椭圆的方程即可.
(II)设出P的坐标,将其代入椭圆的方程得到P的坐标的关系,写出A,B的坐标,利用两点连线的斜率公式求出
k1,k2,将P的坐标的关系代入k1k2化简求出其值.
(III)设出M的坐标,求出P的坐标,利用两点的距离公式将已知的几何条件用坐标表示,通过对参数λ的讨论,判断出M的轨迹.
点评:求圆锥曲线的方程,一般利用待定系数法;解决直线与圆锥曲线的位置关系问题,一般设出直线方程,将直线方程与圆锥曲线方程联立,消去一个未知数,得到关于一个未知数的二次方程,利用韦达定理,找突破口.注意设直线方程时,一定要讨论直线的斜率是否存在.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: