题目内容
【题目】已知函数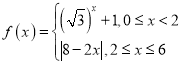
,若函数
有5个零点，则实数
的取值范围是( )
A.
B.
C.
D.
【答案】C
【解析】
画出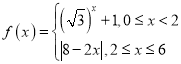
图像,求得函数
的值域为
,函数
有
个零点,故方程
有个实根, 即函数
的图像与直线
有个不同的交点,对
分类讨论,即可求得答案.
画出图像:
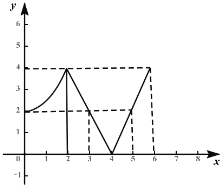
由图可知:函数的值域为
函数有个零点,
方程有个实根
即函数的图像与直线有个不同的交点
①当
或
时,
函数的图像与直线没有交点
故函数的图像与直线没有交点
函数没有零点,与题意不符,故舍去;
②当
时,
函数的图像与直线
只有一个交点
即方程
只有一个实根
令
,得
或
即此时函数只有两个零点
和
,与题意不符,故舍去;
③当
时,
函数的图像与直线有两个交点
即方程
有两个实根
,且
则方程
只有三个实根,而方程
无实根
即此时函数只有三个零点,与题意不符,故舍去;
④当
时,函数的图像与直线
有三个交点
即方程有三个实根
方程有一个实根,方程
有三个实根,方程
无实根
即此时函数有四个零点,与题意不符,故舍去;
⑤当
时,
函数 的图像与直线有三个交点
即方程有三个实根
且
则方程有两个实根,方程有三个实根,方程
无实根
即此时函数只有五个零点,与题意相符合
⑥当
时,
函数的图像与直线
有两个交点
即方程有两个实根,或
方程
有三个实根,方程
无实根
即此时函数有三个零点,与题意不符,故舍去
综上所述,实数的取值范围是
.
故选:C.
名校课堂系列答案
【题目】基于移动网络技术的共享单车被称为“新四大发明”之一，短时间内就风靡全国，给人们带来新的出行体验，某共享单车运营公司的市场研究人员为了了解公司的经营状况，对公司最近6个月的市场占有率
进行了统计，结果如下表：
月份 | 2018.11 | 2018.12 | 2019.01 | 2019.02 | 2019.03 | 2019.04 |
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
| 11 | 13 | 16 | 15 | 20 | 21 |
（1）请用相关系数说明能否用线性回归模型拟合
与月份代码
之间的关系.如果能，请计算出关于的线性回归方程，如果不能，请说明理由；
（2）根据调研数据，公司决定再采购一批单车扩大市场，从成本1000元/辆的
型车和800元/辆的
型车中选购一种，两款单车使用寿命频数如下表：
车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
| 10 | 30 | 40 | 20 | 100 |
| 15 | 40 | 35 | 10 | 100 |
经测算，平均每辆单车每年能为公司带来500元的收入，不考虑除采购成本以外的其它成本，假设每辆单车的使用寿命都是整数年，用频率估计每辆车使用寿命的概率，以平均每辆单车所产生的利润的估计值为决策依据，如果你是公司负责人，会选择哪款车型？
参考数据：
，
，
，
.
参考公式：相关系数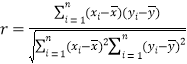
，
，
.
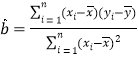