题目内容
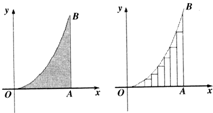 抛物线y=x2,x轴及直线AB:x=1围成如图所示的阴影部分,把线段OA等分成n等份,作以
抛物线y=x2,x轴及直线AB:x=1围成如图所示的阴影部分,把线段OA等分成n等份,作以| 1 |
| n |
| 1 |
| 3 |
| 1 |
| 3 |
分析:求出抛物线与直线AB的交点,可得所求面积为函数x2在区间[0,1]上的定积分的值,再用定积分计算公式加以运算即可得到本题答案.
解答:解:∵抛物线y=x2与直线AB:x=1的交点为A(1,1)
∴由定积分的几何意义,可得所求图形的面积为
S=
x2dx=
x3
=
-0=
故答案为:

∴由定积分的几何意义,可得所求图形的面积为
S=
| ∫ | 1 0 |
| 1 |
| 3 |
| | | 1 0 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题求曲线与x轴及直线x=1围成的曲边图形的面积,着重考查了定积分的几何意义和积分计算公式等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知直线AB:x+y-6=0与抛物线y=x2及x轴正半轴围成的阴影部分如图所示,若从Rt△AOB区域内任取一点M(x,y),则点M取自阴影部分的概率为
已知直线AB:x+y-6=0与抛物线y=x2及x轴正半轴围成的阴影部分如图所示,若从Rt△AOB区域内任取一点M(x,y),则点M取自阴影部分的概率为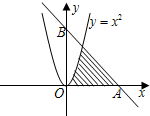 已知直线AB:x+y-6=0与抛物线y=x2及x轴正半轴围成的阴影部分如图所示,若从Rt△AOB区域内任取一点M(x,y),则点M取自阴影部分的概率为________.
已知直线AB:x+y-6=0与抛物线y=x2及x轴正半轴围成的阴影部分如图所示,若从Rt△AOB区域内任取一点M(x,y),则点M取自阴影部分的概率为________.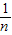 为底的内接矩形,阴影部分的面积S等于这些内接矩形面积之和当n→∞时的极限值,则S的值为 .
为底的内接矩形,阴影部分的面积S等于这些内接矩形面积之和当n→∞时的极限值,则S的值为 .