Question

函数f（x）对一切实数x,y均有f（x+y）-f（y）=（x+2y+1）·x成立，且?f（1）=0.

（1）求f（0）的值；?

（2）当f（x）+2＜log_ax,x∈（0, ）恒成立时，求a的取值范围.?

Answer 1

思路分析：由于x,y，等式恒成立，赋值法求出f（0），不等式恒成立，转化为求函数值域问题.

解：（1）由已知等式?

f（x+y）-f（y）=（x+2y+1）·x,?

令x=1,y=0得f（1）-f（0）=2,又因为f（1）=0，所以?f（0）=-2.?

（2）由（1）知f（0）=-2,所以f（x）+2=f（x）-f（0）=f（x+0）-f（0）=（x+1）·x.

即f（x）=x²+x-2，

“x∈（0,）,f（x）+2＜log_ax恒成立”，?

即为x∈（0,）时，f（x）-log_ax+2＜0恒成立，在x∈（0,）时，f（x）为增函数，-2＜f（x）＜-.?

显然a＞1时，x∈（0,）,log_ax∈（-∞,?-log_a2?），上式恒成立的不等式不可能.?

当0＜a＜1时，x∈（0,），log_ax∈?（-log_a2,+∞）.??

即x∈（0，）时，f（x）-log_ax+2＜+log_a2.?

∵x∈（0,）,f（x）-log_ax+2＜0恒成立，?

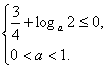∴∴≤a＜1.

温馨提示

题意给出全称命题，显然可以任取x=1，y=0代入.