题目内容
设椭圆 =1(a>b>0)过点
=1(a>b>0)过点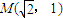 ,且左焦点为
,且左焦点为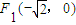
(Ⅰ)求椭圆C的方程;
(Ⅱ)当过点P(4,1)的动直线l与椭圆C相交与两不同点A,B时,在线段AB上取点Q,满足
 •
•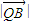 =
=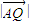 •
•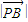 ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上.
【答案】分析:(Ⅰ)通过椭圆焦点坐标知c= ,且有a2=b2+c2,又点M的坐标满足椭圆方程,则列方程组解之即可;
,且有a2=b2+c2,又点M的坐标满足椭圆方程,则列方程组解之即可;
(Ⅱ)欲证点Q总在某定直线上,所以先设点Q的坐标为变量(x,y),点A、B的坐标分别为参数(x1,y1)、(x2,y2),然后根据已知条件可变形得 ,设其比值为λ则有
,设其比值为λ则有 、
、 ,此时利用定比分点定理可得A、B、P三点横坐标关系及纵坐标关系,同时可得A、B、Q三点横坐标关系及纵坐标关系,又因为点A、B的坐标满足椭圆方程,则有x12+2y12=4,x22+2y22=4,再利用已得关系式构造x12+2y12与x22+2y22则可整体替换为4,同时消去参数λ,最后得到变量x、y的关系式,则问题得证.
,此时利用定比分点定理可得A、B、P三点横坐标关系及纵坐标关系,同时可得A、B、Q三点横坐标关系及纵坐标关系,又因为点A、B的坐标满足椭圆方程,则有x12+2y12=4,x22+2y22=4,再利用已得关系式构造x12+2y12与x22+2y22则可整体替换为4,同时消去参数λ,最后得到变量x、y的关系式,则问题得证.
解答:解:(Ⅰ)由题意得 ,
,
解得a2=4,b2=2,
所以椭圆C的方程为 .
.
(Ⅱ)设点Q、A、B的坐标分别为(x,y),(x1,y1),(x2,y2).
由题设知 ,
, ,
, ,
, 均不为零,记
均不为零,记 ,则λ>0且λ≠1
,则λ>0且λ≠1
又A,P,B,Q四点共线,从而
于是 ,
, ,
, ,
,
从而 ①,
①, ②,
②,
又点A、B在椭圆C上,即x12+2y12=4 ③,x22+2y22=4 ④,
①+②×2并结合③、④得4x+2y=4,
即点Q(x,y)总在定直线2x+y-2=0上.
点评:本题综合考查椭圆性质与定比分点定理,同时考查构造消元处理方程组的能力.
 ,且有a2=b2+c2,又点M的坐标满足椭圆方程,则列方程组解之即可;
,且有a2=b2+c2,又点M的坐标满足椭圆方程,则列方程组解之即可;(Ⅱ)欲证点Q总在某定直线上,所以先设点Q的坐标为变量(x,y),点A、B的坐标分别为参数(x1,y1)、(x2,y2),然后根据已知条件可变形得
 ,设其比值为λ则有
,设其比值为λ则有 、
、 ,此时利用定比分点定理可得A、B、P三点横坐标关系及纵坐标关系,同时可得A、B、Q三点横坐标关系及纵坐标关系,又因为点A、B的坐标满足椭圆方程,则有x12+2y12=4,x22+2y22=4,再利用已得关系式构造x12+2y12与x22+2y22则可整体替换为4,同时消去参数λ,最后得到变量x、y的关系式,则问题得证.
,此时利用定比分点定理可得A、B、P三点横坐标关系及纵坐标关系,同时可得A、B、Q三点横坐标关系及纵坐标关系,又因为点A、B的坐标满足椭圆方程,则有x12+2y12=4,x22+2y22=4,再利用已得关系式构造x12+2y12与x22+2y22则可整体替换为4,同时消去参数λ,最后得到变量x、y的关系式,则问题得证.解答:解:(Ⅰ)由题意得
 ,
,解得a2=4,b2=2,
所以椭圆C的方程为
 .
.(Ⅱ)设点Q、A、B的坐标分别为(x,y),(x1,y1),(x2,y2).
由题设知
 ,
, ,
, ,
, 均不为零,记
均不为零,记 ,则λ>0且λ≠1
,则λ>0且λ≠1又A,P,B,Q四点共线,从而

于是
 ,
, ,
, ,
,
从而
 ①,
①, ②,
②,又点A、B在椭圆C上,即x12+2y12=4 ③,x22+2y22=4 ④,
①+②×2并结合③、④得4x+2y=4,
即点Q(x,y)总在定直线2x+y-2=0上.
点评:本题综合考查椭圆性质与定比分点定理,同时考查构造消元处理方程组的能力.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 =1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为
=1(a>b>0)的左、右焦点分别为F1,F2,A是椭圆上的一点,AF2⊥F1F2,原点O到直线AF1的距离为 .
. ;
; +
+ =1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2.
=1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2. =λ1
=λ1 ,
,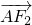 =λ2
=λ2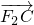 ,当A在椭圆上运动时,求证:λ1+λ2为定值.
,当A在椭圆上运动时,求证:λ1+λ2为定值.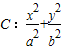 =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
•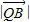 =
=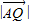 •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上. =1(a>b>0)过点
=1(a>b>0)过点 ,且左焦点为
,且左焦点为
 •
• =
= •
• ,证明:点Q总在某定直线上.
,证明:点Q总在某定直线上. =1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P(
=1(a>b>0)的焦距为2c.以点O为圆心,a为半径作圆M.若过点P( ,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______
,0)所作圆M的两条切线互相垂直,则该椭圆的离心率为______