Question

【题目】如图，在△ABC中，角A，B，C所对的边分别为a，b，c，且3bsinA=c，D为AC边上一点．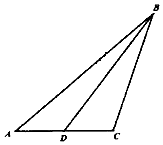

（1）若D是AC的中点，且 ， ，求△ABC的最短边的边长．
（2）若c=2b=4，S△BCD= ，求DC的长．

Answer 1

【答案】
（1）解：在△ABD中，∵ ，3bsinA=c，

∴ ，由余弦定理可得 ，

解得 ．

在△ABC中， ，

解得 ，

∴△ABC的最短边的边长 ；

（2）∵c=2b，∴sinC=2sinB，

由3bsinA=c，得sinAsinB= sinC，∴ ，

∴ ，

由 ，

∴ ．

【解析】1、由已知根据余弦定理可得 b = 2 ， c = 6，在△ABC中，利用大边对大角再根据余弦定理可求出a的值。
2、由正弦定理可知，sinC=2sinB，再由已知条件可得s i n A = ，进而求出 S △ A B C，由面积之比得到之比，即得结果。