题目内容
有一条生产流水线，由于改进了设备，预计第1年的增长率为150％，以后每年的增长率是前一年的一半，设原来的产量为a．写出改进设备后的第1年、第2年、第3年的产量________，________，________．
解析：
|
答案： 解：设改进设备后第n年的产量为an(n∈N)，则a1＝a(1＋150％)＝ a2＝a1(1＋75％)＝ |
a 
a 
a
＝
＝
云南师大附小一线名师提优作业系列答案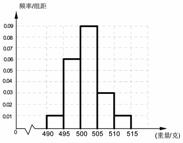
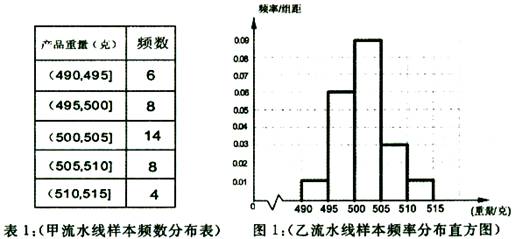
某食品厂为了检查甲乙两条自动包装流水线的生产情况，在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]的产品为合格品，否则为不合格品．表1是甲流水线样本频数分布表，图1是乙流水线样本的频率分布直方图．表1：（甲流水线样本频数分布表）
| 产品重量（克） | 频数 |
| （490，495] | 6 |
| （495，500] | 8 |
| （500，505] | 14 |
| （505，510] | 8 |
| （510，515] | 4 |
（2）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”．
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合计 | n= |
（本小题满分12分）品厂为了检查甲、乙两条自动包装流水线的生产情况，在这两条
流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]
的产品为合格品，否则为不合格品，表1是甲流水线样本频数分布表，图1是乙流水线样
本的频率分布直方图。
某食
（1）若检验员不小心将甲、乙两条流水线生产的重量值在（510，515]的产品放在了一起，
然后又随机取出3件产品，求至少有一件是乙流水线生产的产品的概率；
（2）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量
与两条自动包装流水线的选择有关”。
|
|
甲流水线 |
乙流水线 |
合 计 |
|
合格品 |
a= |
b= |
|
|
不合格品 |
c= |
d= |
|
|
合 计 |
|
|
n= |
（本小题满分12分）
某食品厂为了检查甲乙两条自动包装流水线的生产情况，在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在
的产品为合格品，否则为不合格品。表1是甲流水线样本频数分布表，图1是乙流水线样本的频率分布直方图。
表１：（甲流水线样本频数分布表） 图１：（乙流水线样本频率分布直方图）
（1）若检验员不小心将甲、乙两条流水线生产的重量值在（510，515］的产品放在了一起，然后又随机取出3件产品，求至少有一件是乙流水线生产的产品的概率．
（2）由以上统计数据完成下面２×２列联表，并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”．
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合计 | n= |
表1：（甲流水线样本频数分布表）
| 产品重量（克） | 频数 |
| （490，495] | 6 |
| （495，500] | 8 |
| （500，505] | 14 |
| （505，510] | 8 |
| （510，515] | 4 |
（2）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”．
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合计 | n= |
表1：（甲流水线样本频数分布表）
| 产品重量（克） | 频数 |
| （490，495] | 6 |
| （495，500] | 8 |
| （500，505] | 14 |
| （505，510] | 8 |
| （510，515] | 4 |
（2）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”．
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合计 | n= |
