题目内容
已知函数y=f(x)在定义域(-1+∞)内满足f(0)=0,且f′(x)=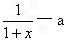 ,(f′(x))是f(x)的导数)
,(f′(x))是f(x)的导数)
(Ⅰ)求f(x)的表达式.
(Ⅱ)当a=1时,讨论f(x)的单调性
(Ⅲ)设h(x)=(ex-P)2+(x-P)2,证明:h(x)≥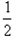
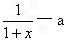 ,(f′(x))是f(x)的导数)
,(f′(x))是f(x)的导数)(Ⅰ)求f(x)的表达式.
(Ⅱ)当a=1时,讨论f(x)的单调性
(Ⅲ)设h(x)=(ex-P)2+(x-P)2,证明:h(x)≥
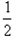
解:(Ⅰ)由f′(x)=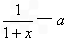 ,可得f(x)=ln(1+x)-ax+b,b为实常数.
,可得f(x)=ln(1+x)-ax+b,b为实常数.
又f(0)=0 b=0.
b=0.
∴f(x)=ln(1+x)-ax.
(Ⅱ)当a=1时,f(x)= ln(1+x)-x. (x>-1)
f′(x)=
∵x>-1 由f′(x)=0 x=0
x=0
∴当x∈(-1,0]时f′(x)≥0,此时f(x)递增
当x∈(0,+∞)时,f′(x)<0,此时f(x)递减
即f(x)在(-1,0)上单调增,在(0,+∞)上单调减
(Ⅲ)由(Ⅱ)知f(x)≤f(0)=0在(-1,+∞)内恒成立
∴ln (1+x) ≤x,∴ex≥1+x ex-x≥1
ex-x≥1
∴(ex-x)2≥1
∴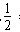 ≤
≤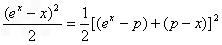 ≤(ex-P)2+(P-x)2
≤(ex-P)2+(P-x)2
即h(x)=(ex-P)2+(P-x)2≥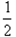
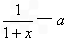 ,可得f(x)=ln(1+x)-ax+b,b为实常数.
,可得f(x)=ln(1+x)-ax+b,b为实常数.又f(0)=0
 b=0.
b=0.∴f(x)=ln(1+x)-ax.
(Ⅱ)当a=1时,f(x)= ln(1+x)-x. (x>-1)
f′(x)=

∵x>-1 由f′(x)=0
 x=0
x=0 ∴当x∈(-1,0]时f′(x)≥0,此时f(x)递增
当x∈(0,+∞)时,f′(x)<0,此时f(x)递减
即f(x)在(-1,0)上单调增,在(0,+∞)上单调减
(Ⅲ)由(Ⅱ)知f(x)≤f(0)=0在(-1,+∞)内恒成立
∴ln (1+x) ≤x,∴ex≥1+x
 ex-x≥1
ex-x≥1 ∴(ex-x)2≥1
∴
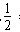 ≤
≤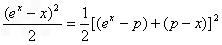 ≤(ex-P)2+(P-x)2
≤(ex-P)2+(P-x)2即h(x)=(ex-P)2+(P-x)2≥
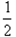

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知函数y=f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
| A、1005 | B、2010 |
| C、2011 | D、4020 |