题目内容
已知函数 满足:对任意实数x1,x2,当x1<x2时,总有f(x1)-f(x2)>0,那么实数a的取值范围是( )
满足:对任意实数x1,x2,当x1<x2时,总有f(x1)-f(x2)>0,那么实数a的取值范围是( )A.

B.

C.

D.

【答案】分析:由已知可得函数 是(-∞,+∞)上的减函数,则分段函数在每一段上的图象都是下降的,且在分界点即x=1时,第一段函数的函数值应大于等于第二段函数的函数值.由此不难判断a的取值范围.
是(-∞,+∞)上的减函数,则分段函数在每一段上的图象都是下降的,且在分界点即x=1时,第一段函数的函数值应大于等于第二段函数的函数值.由此不难判断a的取值范围.
解答:解:∵对任意实数x1,x2,当x1<x2时,总有f(x1)-f(x2)>0,
∴函数 是(-∞,+∞)上的减函数,
是(-∞,+∞)上的减函数,
当x≥1时,y=logax单调递减,
∴0<a<1;
而当x<1时,f(x)=(3a-1)x+4a单调递减,
∴a< ;
;
又函数在其定义域内单调递减,
故当x=1时,(3a-1)x+4a≥logax,得a≥ ,
,
综上可知, ≤a<
≤a< .
.
故选A
点评:分段函数分段处理,这是研究分段函数图象和性质最核心的理念,具体做法是:分段函数的定义域、值域是各段上x、y取值范围的并集,分段函数的奇偶性、单调性要在各段上分别论证;分段函数的最大值,是各段上最大值中的最大者.
 是(-∞,+∞)上的减函数,则分段函数在每一段上的图象都是下降的,且在分界点即x=1时,第一段函数的函数值应大于等于第二段函数的函数值.由此不难判断a的取值范围.
是(-∞,+∞)上的减函数,则分段函数在每一段上的图象都是下降的,且在分界点即x=1时,第一段函数的函数值应大于等于第二段函数的函数值.由此不难判断a的取值范围.解答:解:∵对任意实数x1,x2,当x1<x2时,总有f(x1)-f(x2)>0,
∴函数
 是(-∞,+∞)上的减函数,
是(-∞,+∞)上的减函数,当x≥1时,y=logax单调递减,
∴0<a<1;
而当x<1时,f(x)=(3a-1)x+4a单调递减,
∴a<
 ;
;又函数在其定义域内单调递减,
故当x=1时,(3a-1)x+4a≥logax,得a≥
 ,
,综上可知,
 ≤a<
≤a< .
.故选A
点评:分段函数分段处理,这是研究分段函数图象和性质最核心的理念,具体做法是:分段函数的定义域、值域是各段上x、y取值范围的并集,分段函数的奇偶性、单调性要在各段上分别论证;分段函数的最大值,是各段上最大值中的最大者.

练习册系列答案
相关题目
 满足
满足 ,对任意
,对任意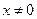 恒成立,在数列
恒成立,在数列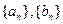 中,
中,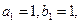 对任意
对任意
 ,总存在自然数k,当
,总存在自然数k,当 时,
时,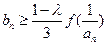 恒成立,求k的最小值。
恒成立,求k的最小值。 满足
满足 ,对任意
,对任意 都有
都有 ,且
,且 .
.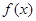 的解析式;
的解析式; ,使函数
,使函数 在
在 上为减函数?若存在,求出实数
上为减函数?若存在,求出实数 满足:①对任意
满足:①对任意 ,恒有
,恒有 成立;②当
成立;②当 时,
时,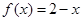 .若
.若
 ,则满足条件的最小的正实数
,则满足条件的最小的正实数 是 .
是 . 满足:①对任意
满足:①对任意 ,恒有
,恒有 成立;②当
成立;②当 时,
时, .若
.若
 ,则满足条件的最小的正实数
,则满足条件的最小的正实数 是 .
是 .