题目内容
已知函数 满足
满足 ,对任意
,对任意 都有
都有 ,且
,且 .
.
(1)求函数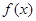 的解析式;
的解析式;
(2)是否存在实数 ,使函数
,使函数 在
在 上为减函数?若存在,求出实数
上为减函数?若存在,求出实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】
(1) ;(2)存在实数
;(2)存在实数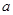 ,
, .
.
【解析】
试题分析:(1)根据 求得
求得 ;
;
根据对任意 ,有
,有 ,确定
,确定 图像的对称轴为直线
图像的对称轴为直线 ,求得
,求得 ;
;
利用对任意 都有
都有 ,转化成
,转化成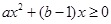 对任意
对任意 成立,解得
成立,解得 .
.
(2)化简函数
 ,其定义域为
,其定义域为 ,
,
令 ,利用复合函数的单调性,得到
,利用复合函数的单调性,得到 求解,得
求解,得 ,肯定存在性.
,肯定存在性.
试题解析:
(1)由 及
及 ∴
∴ 1分
1分
又对任意 ,有
,有
∴ 图像的对称轴为直线
图像的对称轴为直线 ,则
,则 ,∴
,∴ 3分
3分
又对任意 都有
都有 ,
,
即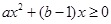 对任意
对任意 成立,
成立,
∴ ,故
,故 6分
6分
∴ 7分
7分
(2)由(1)知
 ,其定义域为
,其定义域为 8分
8分
令
要使函数 在
在 上为减函数,
上为减函数,
只需函数 在
在 上为增函数,
11分
上为增函数,
11分
由指数函数的单调性,有 ,解得
,解得 13分
13分
故存在实数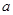 ,当
,当 时,函数
时,函数 在
在 上为减函数 14分
上为减函数 14分
考点:二次函数的图象和性质,待定系数法,复合函数的单调性,对数函数的性质.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
 满足
满足 ,对任意
,对任意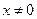 恒成立,在数列
恒成立,在数列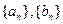 中,
中,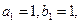 对任意
对任意
 ,总存在自然数k,当
,总存在自然数k,当 时,
时,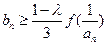 恒成立,求k的最小值。
恒成立,求k的最小值。 满足:①对任意
满足:①对任意 ,恒有
,恒有 成立;②当
成立;②当 时,
时,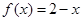 .若
.若
 ,则满足条件的最小的正实数
,则满足条件的最小的正实数 是 .
是 . 满足:①对任意
满足:①对任意 ,恒有
,恒有 成立;②当
成立;②当 时,
时, .若
.若
 ,则满足条件的最小的正实数
,则满足条件的最小的正实数 是 .
是 .