题目内容
在直角坐标平面上给定一曲线y2=2x.(1)设点A的坐标为(![]() ,0),求曲线上距点A最近的点P之坐标及相应的距离|PA|;
,0),求曲线上距点A最近的点P之坐标及相应的距离|PA|;
(2)设点A的坐标为(a,0)a∈R,求曲线上的点到点A距离的最小值d,并写出d=?f(a)的?函数表达式.
解:(1)设M(x,y)为曲线y2=2x上任意一点,则|MA|2=(x-![]() )2+y2=x2+
)2+y2=x2+![]() x+
x+![]() =(x+
=(x+![]() )2+
)2+![]() .
.
因为x∈[0,+∞),?
所以当x=0时,|MA|2min=(![]() )2+
)2+![]() =
=![]() ,?
,?
即|MA|min=23.?
所以距点A最近的点P坐标为(0,0),这时|PA|=![]() .
.
(2)依题设得,
d2=(x-a)2+y2=x2-2ax+a2+2x?
=x2-2(a-1)x+a2?
=[x-(a-1)]2+(2a-1),?
因为x∈[0,+∞),?
所以分a-1≥0和a-1<0两种情况讨论.?
当a≥1时,dmin2=2a-1,?
即dmin=![]() ;?
;?
当a<1时,dmin2=[0-(a-1)]2+(2a-1)=a2,
即dmin=|a|,这时恰好抛物线顶点(0,0)与点A(a,0)最近.?
所以d=f(a)=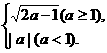

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目