题目内容
甲、乙两名教师进行乒乓球比赛,采用七局四胜制(先胜四局者获胜).若每一局比赛甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为 ,现已赛完两局,乙暂时以2∶0领先.
,现已赛完两局,乙暂时以2∶0领先.
(1)求甲获得这次比赛胜利的概率;
(2)设比赛结束时比赛的局数为随机变量X,求随机变量X的概率分布和数学期望EX.
 ,乙获胜的概率为
,乙获胜的概率为 ,现已赛完两局,乙暂时以2∶0领先.
,现已赛完两局,乙暂时以2∶0领先.(1)求甲获得这次比赛胜利的概率;
(2)设比赛结束时比赛的局数为随机变量X,求随机变量X的概率分布和数学期望EX.
(1) 甲获得这次比赛胜利的概率为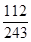 ;(2) X的概率分布为:
;(2) X的概率分布为:
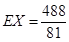 .
.
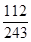 ;(2) X的概率分布为:
;(2) X的概率分布为:| X | 4 | 5 | 6 | 7 |
| P | ?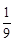 | ?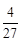 | ?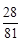 | ?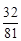 |
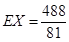 .
.试题分析:(1)甲获得这次比赛胜利情况有二,一是比赛六局结束,甲连续赢了四局,一是比赛了七局,甲在后五局中赢了四局,且最后一局是甲赢,显然这两种情况彼此互斥,故分别计算出这两个事件的概率,求其和即得甲获得这次比赛胜利的概率.(2)设比赛结束时比赛的局数为
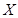 ,由题意得随机变量
,由题意得随机变量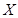 可能的取值为4,5,6,7,分别求出随机变量
可能的取值为4,5,6,7,分别求出随机变量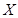 的概率,从而得分布列和数学期望.本题考查
的概率,从而得分布列和数学期望.本题考查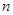 次独立重复试验中恰好发生
次独立重复试验中恰好发生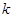 次的概率,解题的关键是正确理解两个事件、“甲获得这次比赛胜利”,再由概率的计算公式计算出概率.本题是概率中的有一定综合性的题,对事件正确理解与分类是很关键.
次的概率,解题的关键是正确理解两个事件、“甲获得这次比赛胜利”,再由概率的计算公式计算出概率.本题是概率中的有一定综合性的题,对事件正确理解与分类是很关键.试题解析:(1)设甲获胜为事件A,则甲获胜包括甲以4∶2获胜和甲以4∶3获胜两种情况.
设甲以4∶2获胜为事件A1,则
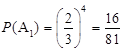 2分
2分设甲以4∶3获胜为事件A2,则
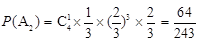 5分
5分P(A)=
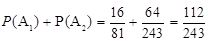 . 6分
. 6分(2)随机变量
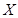 可能的取值为4,5,6,7,
可能的取值为4,5,6,7,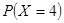 =
=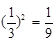 .
.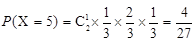 .
.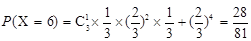 .
.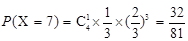 .
.X的概率分布为:
| X | 4 | 5 | 6 | 7 |
| P | ?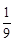 | ?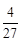 | ?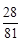 | ?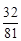 |
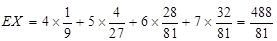 12分
12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的社长是高中学生,
的社长是高中学生, 的社长是初中学生,高中社长中有
的社长是初中学生,高中社长中有 是高一学生,初中社长中有
是高一学生,初中社长中有 是初二学生.
是初二学生. ,求
,求 .
.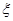 为取得红球的个数.
为取得红球的个数. 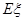 .
.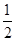 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是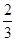 ,假设各局比赛结果相互独立.
,假设各局比赛结果相互独立. 则X的分布列为________.
则X的分布列为________. ,甲、丙二人都回答错的概率是
,甲、丙二人都回答错的概率是 ,乙、丙二人都回答对的概率是
,乙、丙二人都回答对的概率是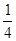 .
.


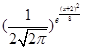 (x∈R),则E(2X-1)=( ).
(x∈R),则E(2X-1)=( ).