题目内容
等差数列{an}的公差为3,若a2, a4,a8成等比数列,则a4=( )
| A.8 | B.10 | C.12 | D.16 |
C
解析

练习册系列答案
相关题目
设等差数列 的前n项和为
的前n项和为 ,若
,若 ,则必定有
,则必定有
A. | B. |
C. | D. |
已知数列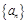 的前
的前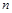 项和为
项和为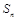 ,并满足:
,并满足: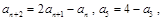 则
则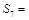 ( )
( )
| A.7 | B.12 | C.14 | D.21 |
等差数列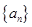 ,
,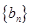 的前
的前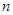 项和分别为
项和分别为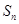 ,
,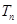 ,若
,若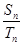
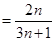 ,则
,则 ( )
( )
A.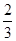 | B.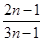 | C.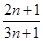 | D. |
等差数列 中,
中,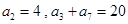 ,则
,则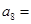 ( )
( )
| A.8 | B.12 | C.16 | D.24 |
记Sn是等差数列{an}前n项的和,Tn是等比数列{bn}前n项的积,设等差数列{an}公差d≠0,若对小于2011的正整数n,都有Sn=S2011-n成立,则推导出a1006=0.设等比数列{bn}的公比q≠1,若对于小于23的正整数n,都有Tn=T23-n成立,则( )
| A.b11=1 | B.b12=1 | C.b13=1 | D.b14=1 |
已知数列{an},{bn}满足a1=b1=3,an+1-an= =3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
=3,n∈N*,若数列{cn}满足cn=ban,则c2 013=( )
| A.92 012 | B.272 012 |
| C.92 013 | D.272 013 |
下面是关于公差d>0的等差数列{an}的四个命题:
p1:数列{an}是递增数列;p2:数列{nan}是递增数列;
p3:数列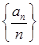 是递增数列;p4:数列{an+3nd}是递增数列.
是递增数列;p4:数列{an+3nd}是递增数列.
其中的真命题为( ).
| A.p1,p2 | B.p3,p4 |
| C.p2,p3 | D.p1,p4 |

