题目内容
(本小题满分12分)已知 是定义在R上的偶函数,且
是定义在R上的偶函数,且 时,
时, .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若
 的取值范围.
的取值范围.
(1) ;(2)(-∞, 0)
;(2)(-∞, 0) (2, +∞).
(2, +∞).
【解析】
试题分析:
(Ⅰ)令x>0,则-x<0,
从而 ,
,
∴x>0时, .
.
∴函数f(x)的解析式为 .
.
(Ⅱ)设 是任意两个值,且
是任意两个值,且 ,
,
则 ,∴
,∴ .
.
∵ ,
,
∴ ,
,
∴ 在(-∞, 0]上为增函数.又f(x)是定义在R上的偶函数,
在(-∞, 0]上为增函数.又f(x)是定义在R上的偶函数,
∴f(x)在(0, +∞)上为减函数.
∵f(a-1)<-1=f(1),∴|a-1|>1,解得a>2或a<0.
故实数a的取值范围为(-∞, 0) (2, +∞).
(2, +∞).
考点:考查了求函数的解析式,利用函数的单调性解不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
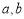 ,两个平面
,两个平面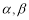 .给出下面四个命题:( )
.给出下面四个命题:( )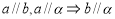 ;
; 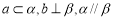
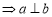 ;
;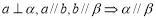 ;
; 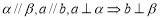 .
. 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,则“
,则“ ”是“
”是“ ”的( )
”的( )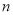 的值为
的值为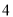 ,则输出
,则输出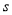 的值为____________.
的值为____________.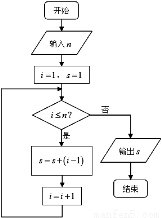
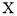 的分布列为
的分布列为







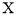 的数学期望
的数学期望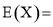 ( )
( )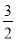 B.
B.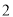 C.
C. D.
D.
 是定义在R上的偶函数,并满足
是定义在R上的偶函数,并满足 ,当
,当
 ,则
,则
 __________.
__________. (其中A>0,
(其中A>0, )的图像如图所示,为了得到
)的图像如图所示,为了得到 的图像,则只要将
的图像,则只要将 的图像( )
的图像( )
 个单位长度
个单位长度 个单位长度
个单位长度  个单位长度
个单位长度  个单位长度
个单位长度  ,B(5,1),则以线段AB为直径的圆的方程的一般式
,B(5,1),则以线段AB为直径的圆的方程的一般式