题目内容
已知函数 的定义域为R,其导函数
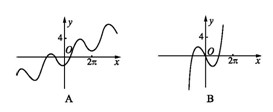
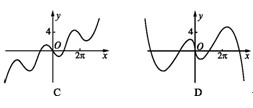
的定义域为R,其导函数 的图像如图所示,则对于任意
的图像如图所示,则对于任意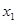 ,
,
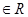 (
(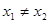 ),下列结论正确的是( )
),下列结论正确的是( )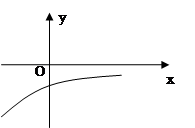
① <0恒成立 ②
<0恒成立 ②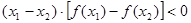 ;③
;③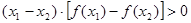 ;
;
④ ;⑤
;⑤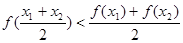 。
。
| A.①③ | B.①③④ | C.②④ | D.②⑤ |
D
解析试题分析:由导函数的图象可知,导函数f′(x)的图象在x轴下方,即f′(x)<0,故原函数为减函数,并且是,递减的速度是先快后慢.由此可得函数f(x)的图象,再结合函数图象易得正确答案.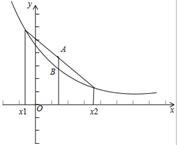
解:由导函数的图象可知,导函数f′(x)的图象在x轴下方,即f′(x)<0,故原函数为减函数,并且是,递减的速度是先快后慢.所以f(x)的图象如图所示. f(x)<0恒成立,没有依据,故①不正确;②表示(x1-x2)与[f(x1)-f(x2)]异号,即f(x)为减函数.故②正确;③表示(x1-x2)与[f(x1)-f(x2)]同号,即f(x)为增函数.故③不正确,④⑤左边边的式子意义为x1,x2中点对应的函数值,即图中点B的纵坐标值,右边式子代表的是函数值得平均值,即图中点A的纵坐标值,显然有左边小于右边,故④不正确,⑤正确,综上,正确的结论为②⑤.故选D.
考点:导数的运用
点评:本题为导函数的应用,由导函数的图象推出原函数应具备的性质,利用数形结合是解决问题的关键,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数 的一个单调递增区间是( )
的一个单调递增区间是( )
A. | B. | C. | D. |
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
当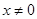 时,有不等式( )
时,有不等式( )
A.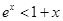 |
B.当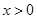 时 时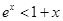 ,当 ,当 时 时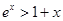 |
C.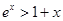 |
D.当 时 时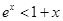 ,当 ,当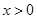 时 时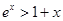 |
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
| A.(1,2) | B.(e,3) | C.(2,e) | D.(e, +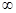 ) ) |
在下列区间中,函数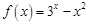 的零点所在区间是( )
的零点所在区间是( )
A.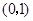 | B.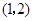 | C.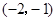 | D.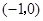 |
设函数 是定义在
是定义在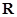 上的以
上的以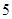 为周期的偶函数,若
为周期的偶函数,若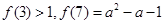 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A.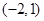 | B.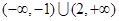 | C.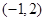 | D.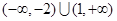 |
设f(x)是定义在R上的奇函数,且f(2)=0,当x>0时,有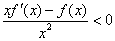 恒成立,则不等式
恒成立,则不等式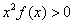 的解集是
的解集是
| A.(-2,0) ∪(2,+∞) | B.(-2,0) ∪(0,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-∞,-2)∪(0,2) |
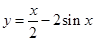 的图象大致是( )
的图象大致是( )