题目内容
设数列{xn}各项均为正数，且满足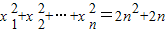
（1）求通项xn
（2）已知
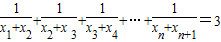，求n的值．
【答案】分析：（1）根据等式满足
，将n换为n-1后两式相减，即可求解；
（2）由（1）求得通项xn，代入
根据分子有理化，对其进行化简，再进行证明；
解答：解：（1）数列{xn}各项均为正数，且满足
①
∴
②
①-②得，xn2=2n2+2n-[2（n-1）2+2（n-1）]=4n，∵数列{xn}各项均为正数，
∴xn=2
；
（2）∵xn=2
；
∴
=
=
（
-
），
=
（
-1+
+••+
）=
×（
）=3，
解得n=48；
点评：此题主要考查数列的求和问题，注意利用好分子有理化进行化简，此题是一道中档题，考查的知识点比教单一；
，将n换为n-1后两式相减，即可求解；（2）由（1）求得通项xn，代入
根据分子有理化，对其进行化简，再进行证明；解答：解：（1）数列{xn}各项均为正数，且满足
①∴
②①-②得，xn2=2n2+2n-[2（n-1）2+2（n-1）]=4n，∵数列{xn}各项均为正数，
∴xn=2
；（2）∵xn=2
；∴
==（-），=（-1++••+）=×（）=3，解得n=48；
点评：此题主要考查数列的求和问题，注意利用好分子有理化进行化简，此题是一道中档题，考查的知识点比教单一；
练习册系列答案
相关题目
(an-an-1)x2-(an+1-an)x(n≥2)取得极值.
时,数列{bn}中是否存在最大项.若存在,是第几项?若不存在,请说明理由.
=2(a＞0且a≠1),设y3=18,y6=12.
,求证:对任意正整数n,总有Tn＜2;
an+1(n∈N*),求数列{lncn}中的最大项.
)n,n∈N*,且x1=1.设an=
xn
,且T2n=a1+2a2+3a3+…+ (2n-1)a2n-1+2na2n.
(n∈N*),试比较9T2n与Qn的大小,并说明理由.
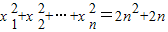
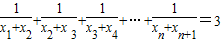，求n的值．