Question

已知定义域为R的函数f(x)=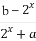是奇函数.

(1)求a,b的值.

(2)用定义证明f(x)在(-∞,+∞)上为减函数.

(3)若对于任意t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的范围.

 

Answer 1

(1) a=1,b=1 (2)见解析 (3) k<-

【解析】(1)∵f(x)为R上的奇函数,∴f(0)=0,b=1.

又f(-1)=-f(1),得a=1.

经检验a=1,b=1符合题意.

(2)任取x1,x2∈R,且x1<x2,

则f(x1)-f(x2)=-

=

=.

∵x1<x2,∴->0,

又∵(+1)(+1)>0,

∴f(x1)-f(x2)>0,

∴f(x)在(-∞,+∞)上为减函数.

(3)∵t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,

∴f(t2-2t)<-f(2t2-k).

∵f(x)为奇函数,∴f(t2-2t)<f(k-2t2),

∵f(x)为减函数,∴t2-2t>k-2t2,

即k<3t2-2t恒成立,而3t2-2t=3(t-)2-≥-,∴k<-.