题目内容
【题目】椭圆![]() 焦点在
焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,上焦点到上顶点距离为
,上焦点到上顶点距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 与椭圆
与椭圆![]() 交与
交与![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() 的面积
的面积![]() ,则
,则![]() 是否为定值,若是求出定值;若不是,说明理由.
是否为定值,若是求出定值;若不是,说明理由.
【答案】(1)![]() (2)
(2)![]() 为定值5.
为定值5.
【解析】
(1)运用椭圆的离心率公式和两点的距离公式,及![]() 的关系,解得
的关系,解得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)设![]() ,讨论直线
,讨论直线![]() 的斜率不存在和存在,设出直线方程,代入椭圆方程,运用韦达定理和判别式大于
的斜率不存在和存在,设出直线方程,代入椭圆方程,运用韦达定理和判别式大于![]() ,结合三角形的面积公式,点到直线的距离公式和弦长公式,化简整理,即可得到所求和为定值5.
,结合三角形的面积公式,点到直线的距离公式和弦长公式,化简整理,即可得到所求和为定值5.
(1)由题意可得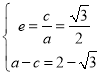 ,
,
解得![]() ,
,
可得![]() ,
,
即有椭圆![]() 的标准方程为:
的标准方程为:![]() ;
;
(2)设![]() ,
,
(1)当![]() 斜率不存在时,
斜率不存在时,![]() 两点关于
两点关于![]() 轴对称,
轴对称,
![]() ,
,
又![]() ,解得
,解得![]() ,
,
![]() ;
;
(2)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由题意知![]() ,将其代入
,将其代入![]() ,得
,得
![]() ,
,
即有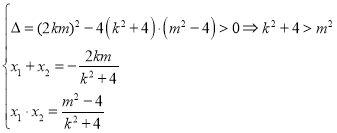 ,
,
则![]() ,
,![]() 到
到![]() 距离
距离![]() ,
,
则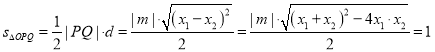 ,
,
解得![]() ,满足
,满足![]() ,
,
则![]() ,
,
即有![]() ,
,
![]()
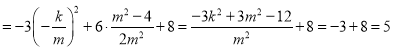 ,
,
综上可得![]() 为定值5.
为定值5.

练习册系列答案
相关题目
【题目】由中央电视台综合频道![]() 和唯众传媒联合制作的
和唯众传媒联合制作的![]() 开讲啦
开讲啦![]() 是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了A、B两个地区的100名观众,得到如表的
是中国首档青年电视公开课,每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了A、B两个地区的100名观众,得到如表的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是B地区当中“非常满意”的观众的概率为
列联表,已知在被调查的100名观众中随机抽取1名,该观众是B地区当中“非常满意”的观众的概率为![]() .
.
非常满意 | 满意 | 合计 | |
A | 30 | 15 | |
B | |||
合计 |
![]() 完成上述表格并根据表格判断是否有
完成上述表格并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系;
的把握认为观众的满意程度与所在地区有关系;
![]() 若以抽样调查的频率为概率,从A地区随机抽取3人,设抽到的观众“非常满意”的人数为X,求X的分布列和期望.
若以抽样调查的频率为概率,从A地区随机抽取3人,设抽到的观众“非常满意”的人数为X,求X的分布列和期望.
|
|
|
|
|
|
|
|
附:参考公式:![]() .
.