题目内容
设x<y,不等式
思路解析:利用函数的观点,即求 解法一:显然a>0.由题意,不等式a≥ 则a必须大于或等于 而( ∴ 解法二:∵ ∴令 则 又由已知,得a≥
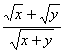 的最大值.
的最大值.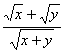 恒成立.
恒成立.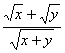 的最大值.
的最大值.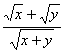 )2=
)2=![]() =1+
=1+![]() ≤2,当且仅当x=y时,取“=”,
≤2,当且仅当x=y时,取“=”,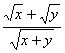 的最大值为
的最大值为![]() ,故a≥2,即a的最小值是
,故a≥2,即a的最小值是![]() .
.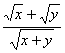 =
=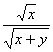 +
+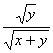 ,又∵(
,又∵(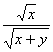 )2+(
)2+(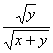 )2=1,
)2=1,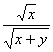 =cosθ,
=cosθ, 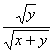 =sinθ(θ∈[0,
=sinθ(θ∈[0, ![]() ]).
]).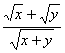 =cosθ+sinθ=
=cosθ+sinθ=![]() sin(θ+
sin(θ+![]() )≤
)≤![]() (当θ=
(当θ=![]() 时取等号),即
时取等号),即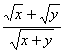 的最大值为
的最大值为![]() .
.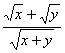 恒成立,∴a≥
恒成立,∴a≥![]() ,即a的最小值为
,即a的最小值为![]() .
. 练习册系列答案
练习册系列答案
远航教育期末夺冠测试卷系列答案
期末突破名牌中学一卷通系列答案
全效测评系列答案
同步三练系列答案
全能测控口算题卡系列答案
学与练全程卷王系列答案
湘教考苑单元整合与测评系列答案
小学毕业升学总复习夺冠小状元系列答案
模拟试卷及真题精选系列答案
 相关题目
相关题目
 则z=3x-2y的最大值是( )
则z=3x-2y的最大值是( ) 则z=3x-2y的最大值是( )
则z=3x-2y的最大值是( )