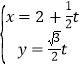题目内容
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求曲线C的极坐标方程和直线l的直角坐标方程;
(2)若射线![]() 与曲线C交于点A(不同于极点O),与直线l交于点B,求
与曲线C交于点A(不同于极点O),与直线l交于点B,求![]() 的最大值.
的最大值.
【答案】(1)![]() :
:![]() ,直线
,直线![]() :
:![]() ;(2)
;(2)![]() .
.
【解析】
(1)由消参法把参数方程化为普通方程,再由公式![]() 进行直角坐标方程与极坐标方程的互化;
进行直角坐标方程与极坐标方程的互化;
(2)由极径的定义可直接把![]() 代入曲线
代入曲线![]() 和直线
和直线![]() 的极坐标方程,求出极径
的极坐标方程,求出极径![]() ,把比值
,把比值![]() 化为
化为![]() 的三角函数,从而可得最大值、
的三角函数,从而可得最大值、
(1)消去参数![]() 可得曲线
可得曲线![]() 的普通方程是
的普通方程是![]() ,即
,即![]() ,代入
,代入![]() 得
得![]() ,即
,即![]() ,∴曲线
,∴曲线![]() 的极坐标方程是
的极坐标方程是![]() ;
;
由![]() ,化为直角坐标方程为
,化为直角坐标方程为![]() .
.
(2)设![]() ,则
,则![]() ,
, ,
,

![]()
![]() ,
,
当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某厂能够生产甲、乙两种产品,已知生产这两种产品每吨所需的煤、电以及每吨的产值分别是:
用煤(t) | 用电(kw) | 产值(千元) | |
甲种产品 | 70 | 20 | 80 |
乙种产品 | 30 | 50 | 110 |
如果该厂每月至多供煤560t,供电450kw,问如何安排生产,才能使该厂月产值最大?月产值是多少?