题目内容
已知数列{an},{bn}是各项均为正数的等比数列,设cn= ,n∈N*
,n∈N*
(Ⅰ)证明:数列{cn}是等比数列,数列{lnan}是等差数列.
(Ⅱ)设数列{lnan},{lnbn}的前n项和分别是Sn,Tn.若a1=2,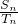 =
= ,求数列{cn}的通项公式.
,求数列{cn}的通项公式.
(Ⅲ)在(Ⅱ)条件下,设dn=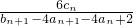 ,求数列{dn}的前n项和.
,求数列{dn}的前n项和.
解:(1)设数列{an}、bn的公比分别为p、q(p>0,q>0),
则由题意可得 ,
,
∴ ,c1=a1•b1
,c1=a1•b1
所以数列cn以a1•b1为首项,以pq为公比的等比数列
又因为 ,
,
数列lnan以lna1为首项,以lnp为公差的等差数列
(2)由题意可得 ,
,
∴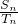 =
= =
=
∴
∴
∴p=4,q=16,b1=8
∴an=2•4n-1=22n-1,bn=8•16n-1=24n-1
(III)由(II)可得
=
=
=
∴d1+d2+d3+…+dn
=
=
分析:(I)根据已知条件可设 ,要证明数列cn为等比数列只要证明
,要证明数列cn为等比数列只要证明 ;要证数列lnan为等差数列,只要证
;要证数列lnan为等差数列,只要证 为常数
为常数
(II)利用(I)的条件可知数列lnanlnbn都为等差数列,代入等差数列的和公式整理可得 ,根据对应项相等可得p、q、b1,进而求出an,bn
,根据对应项相等可得p、q、b1,进而求出an,bn
(III)代入(II)中的条件整理可得 ,用裂项求和的方法可得结果.
,用裂项求和的方法可得结果.
点评:本题主要考查了等差数列、等比数列的定义及判定,考查了等差数列前n项和公式的理解和运用及数列求和中的裂项求和的方法,裂项后要注意相消的项及余下的项的规律.
则由题意可得
 ,
,∴
 ,c1=a1•b1
,c1=a1•b1所以数列cn以a1•b1为首项,以pq为公比的等比数列
又因为
 ,
,数列lnan以lna1为首项,以lnp为公差的等差数列
(2)由题意可得
 ,
,
∴
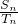 =
= =
=
∴

∴

∴p=4,q=16,b1=8
∴an=2•4n-1=22n-1,bn=8•16n-1=24n-1
(III)由(II)可得

=

=

=

∴d1+d2+d3+…+dn
=

=

分析:(I)根据已知条件可设
 ,要证明数列cn为等比数列只要证明
,要证明数列cn为等比数列只要证明 ;要证数列lnan为等差数列,只要证
;要证数列lnan为等差数列,只要证 为常数
为常数(II)利用(I)的条件可知数列lnanlnbn都为等差数列,代入等差数列的和公式整理可得
 ,根据对应项相等可得p、q、b1,进而求出an,bn
,根据对应项相等可得p、q、b1,进而求出an,bn(III)代入(II)中的条件整理可得
 ,用裂项求和的方法可得结果.
,用裂项求和的方法可得结果.点评:本题主要考查了等差数列、等比数列的定义及判定,考查了等差数列前n项和公式的理解和运用及数列求和中的裂项求和的方法,裂项后要注意相消的项及余下的项的规律.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目