��Ŀ����
ij������һ����ɫˮ������ʱ���ܳ���5���£�Ԥ�����г��ںͺ��ڻ���Ӧ��ʹ�۸����������̬�ƣ��������ֽ����ֹ�������ʹ�۸������µ����������ּ۸�ģ�⺯������f(x)=p��qx;
��f(x)=logqx+p;
��f(x)=(x-1)(x-q)2+p(������ʽ��p��q��Ϊ��������q��2).
(1)Ϊȷ�о���۸����ƣ�Ӧѡ���ּ۸�ģ�⺯����Ϊʲô��
(2)��f(1)=4,f(3)=6,�����ѡ����f(x)�Ľ���ʽ(ע�������Ķ������ǣ�1��6��.����x=1����ʾ4����1���գ�x=2����ʾ5����1���գ�x=3����ʾ6����1���գ������Դ�����)��
(3)Ϊ��֤��ũ�����棬�����ڼ۸��µ��ڼ�����ؿ���·������Ԥ���ˮ�����ļ������ڼ۸��µ�.
(��)ij������һ����ɫˮ������ʱ���ܳ���5���£�Ԥ�����г��ںͺ��ڻ���Ӧ��ʹ�۸����������̬�ƣ��������ֽ����ֹ�������ʹ�۸������µ����������ּ۸�ģ�⺯����
��f(x)=4x;��f(x)=log4x;
��f(x)=(x-1)(x-4)2+4
(�����������Ķ������ǣ�1��6��.����x=1����ʾ4����1���գ�x=2����ʾ5����1���գ�x=3����ʾ6����1���գ������Դ�����).
(1)Ϊȷ�о���۸����ƣ�Ӧѡ���ּ۸�ģ�⺯����Ϊʲô��
(2)Ϊ��֤��ũ�����棬�����ڼ۸��µ��ڼ�����ؿ���·������Ԥ���ˮ�����ļ������ڼ۸��µ�.
�𰸣�(��)�⣺(1)����֪ˮ���ļ۸������ǣ����µ���Ȼ���ٴ����ǣ���ӳ��������ͼ���Ͼ��ǣ����������������Ǽ�����������������.
�ߢ�f(x)=p��qx�ǵ�������������
��f(x)=logqx+p�ǵ�������������
��f(x)=(x-1)(x-q)2+p��f��(x)=3x2-(4q+2)x+q2+2q��
��f��(x)=0,��x1=q,x2=![]() ,f(x)��������㣬���е������䣬���еݼ����䣬
,f(x)��������㣬���е������䣬���еݼ����䣬
��Ӧѡf(x)=(x-1)(x-q)2+pΪ��ģ�⺯��.
(2)��f(1)=4,f(3)=6,�� ,
,
��֮,��![]() (����q=2��ȥ).��f(x)=(x-1)(x-4)2+4=x3-9x2+24x-12(1��x��6).
(����q=2��ȥ).��f(x)=(x-1)(x-4)2+4=x3-9x2+24x-12(1��x��6).
(3)��f��(x)=3x2-18x+24��0,���2��x��4,
�ຯ��f(x)=(x-1)(x-4)2+4=x3-9x2+24x-12������(2��4)�ϵ����ݼ�.�����ֹ�Ʒ��5��6�·ݼ۸������µ�.
(��)�⣺(1)����֪ˮ���ļ۸������ǣ����µ���Ȼ���ٴ����ǣ���ӳ��������ͼ���Ͼ��ǣ����������������Ǽ�����������������.
�ߢ�f(x)=4x�ǵ�����������,��f(x)=log4x�ǵ�������������
��f(x)=(x-1)(x-4)2+4��f��(x)=3x2-18x+24����f��(x)=0,��x1=4,x2=2,
f(x)��������㣬���е������䣬���еݼ����䣬��Ӧѡf(x)=(x-1)(x-4)2+4Ϊ��ģ�⺯��.
(2)��f��(x)=3x2-18x+24��0,���2��x��4��
�ຯ��f(x)=(x-1)(x-4)2+4=x3-9x2+24x-12������(2��4)�ϵ����ݼ�.
�����ֹ�Ʒ��5��6�·ݼ۸������µ�.

| A��f��x��=p•qx | B��f��x��=px2+qx+1 | C��f��x��=plnx+qx2 | D��f��x��=x��x-q��2+p |
 ����
���� ����
����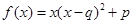 ����������ʽ��
����������ʽ��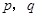 ��Ϊ��������
����������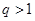 ��
��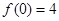 ��
��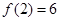 �������ѡ����
�������ѡ����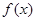 �Ľ���ʽ��ע�������Ķ�������
�Ľ���ʽ��ע�������Ķ������� ��������
��������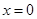 ��ʾ4��1�գ�
��ʾ4��1�գ�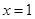 ��ʾ5��1�գ������������ƣ�
��ʾ5��1�գ������������ƣ�