题目内容

若直线y=kx+1与曲线y=|x|有两个交点，则k的取值范围是
（-1，1）
（-1，1）
．
分析：作出直线y=kx+1与曲线y=|x|的图象：利用直线y=kx+1与曲线y=|x|有两个交点，即可得出．
解答：解：作出直线y=kx+1与曲线y=|x|的图象：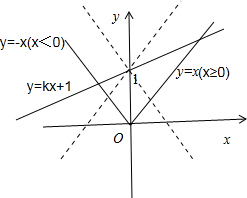
∵直线y=kx+1与曲线y=|x|有两个交点，
∴-1＜k＜1．
故答案为（-1，1）．
点评：本题考查了函数的图象、两条直线的交点问题、数形结合等基础知识与基本技能方法，属于基础题．
练习册系列答案
相关题目
若直线y=kx+1与圆x2+y2=1相交于P、Q两点，且∠POQ=120°（其中O为原点），则k的值为（　　）
A、-
3
或
3
B、
3
C、-
2
或
2
D、
2
已知双曲线C的两个焦点分别为F1(-2
2
，0)、F2(2
2
，0)，双曲线上一点P到F1、F2的距离的差的绝对值等于4．
（Ⅰ）求双曲线的标准方程；
（Ⅱ）若直线y=kx-1与双曲线C没有公共点，求实数k的取值范围．
已知函数f（x）=ex，x∈R．
（Ⅰ）若直线y=kx+1与f（x）的反函数的图象相切，求实数k的值；
（Ⅱ）设x＞0，讨论曲线y=
f(x)
x2
与直线y=m（m＞0）公共点的个数；
（Ⅲ）设a＜b，比较f(
a+b
2
)，
f(b)-f(a)
b-a
的大小，并说明理由．
已知一焦点在x轴上，中心在原点的双曲线的实轴等于虚轴，且图象经过点
2，
3
．
（1）求该双曲线的方程；
（2）若直线y=kx+1与该双曲线只有一个公共点，求实数k的值．
（2013•陕西）已知函数f（x）=ex，x∈R．
（Ⅰ） 若直线y=kx+1与f（x）的反函数的图象相切，求实数k的值；
（Ⅱ） 设x＞0，讨论曲线y=f（x）与曲线y=mx2（m＞0）公共点的个数．
（Ⅲ） 设a＜b，比较
f(a)+f(b)
2
与
f(b)-f(a)
b-a
的大小，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网