Question

某家具厂有方木料90m³，五合板600m²，准备加工成书桌和书橱出售．已知生产每张书桌需要方木料0．1m³，五合板2m²，生产每个书橱需要方木料0．2m²，五合板1m²，出售一张方桌可获利润80元，出售一个书橱可获利润120元．

       （1）如果只安排生产书桌，可获利润多少？

       （2）怎样安排生产可使所得利润最大？

Answer 1

由题意可画表格如下：

	方木料（m3）	五合板（m2）	利润（元）
书桌（个）	0．1	2	80
书橱（个）	0．2	1	120

…………………………………………………………………2分

       （1）设只生产书桌x个，可获得利润z元，

则  ∴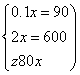 

∴x≤300． ………………………………………………………………4分

所以当x＝300时，z_max＝80×300＝24000（元），即如果只安排生产书桌，最多可生产300张书桌，获得利润24000元．…………………………………………………………6分

（2）设生产书桌x张，书橱y个，利润总额为z元．

则∴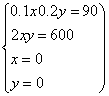

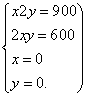
z＝80x＋120y． ………………………………8分

在直角坐标平面内作出上面不等式组所表示的平面区域，即可行域．………………10分

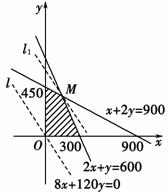
作直线l：80x＋120y＝0，即直线l：2x＋3y＝0．

把直线l向右上方平移至l₁的位置时，直线经过可行域上的点M，

此时z＝80x＋120y取得最大值．………………………………………………12分

由解得点M的坐标为（100,400）．

∴当x＝100，y＝400时，z_max＝80×100＋120×400＝56000（元）．

因此，生产书桌100张、书橱400个，可使所得利润最大．………………………………………14分