题目内容
已知椭圆的方程为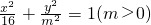 ,如果直线
,如果直线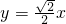 与椭圆的一个交点M在x轴的射影恰为椭圆的右焦点F,则椭圆的离心率为 ________.
与椭圆的一个交点M在x轴的射影恰为椭圆的右焦点F,则椭圆的离心率为 ________.
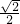
分析:根据椭圆的方程表示出c,得到F的坐标,由直线与椭圆的一个交点M在x轴的射影恰为椭圆的右焦点F得到MF⊥x轴,即F的横坐标与M的横坐标相等,代入直线求出M的纵坐标,把M的坐标代入椭圆方程即可求出m2,利用a2-b2=c2,求出c的值,再求出a根据椭圆离心率e=
 求出即可.
求出即可.解答:由椭圆方程得到右焦点的坐标为(
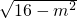 ,0),
,0),因为直线与椭圆的一个交点M在x轴的射影恰为椭圆的右焦点F得到MF⊥x轴,
所以M的横坐标为
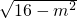 ,代入到直线方程得到M的纵坐标为
,代入到直线方程得到M的纵坐标为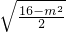 ,则M(
,则M(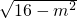 ,
,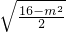 )
)把M的坐标代入椭圆方程得:
 ,化简得:(m2)2+8m2-128=0即(m2-8)(m2+16)=0
,化简得:(m2)2+8m2-128=0即(m2-8)(m2+16)=0解得m2=8,m2=-16(舍去),根据c=
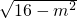 =
=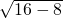 =2
=2 ,而a=
,而a=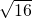 =4
=4所以椭圆的离心率e=
 =
= =
=
故答案为:

点评:考查学生会求直线与椭圆的交点坐标,掌握椭圆的一些简单的性质.

练习册系列答案
相关题目
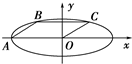 如图所示,已知椭圆的方程为
如图所示,已知椭圆的方程为 的方程为
的方程为 ,双曲线
,双曲线 的两条渐近线为
的两条渐近线为 、
、 .过椭圆
.过椭圆 作直线
作直线 ,使
,使 ,又
,又 交于点
交于点 ,设
,设 、
、 .
.
 与
与 ,且双曲线的焦距为
,且双曲线的焦距为 ,求椭圆
,求椭圆 的最大值.
的最大值.  ,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
,A为椭圆的左顶点,B,C在椭圆上,若四边形OABC为平行四边形,且∠OAB=45°,则椭圆的离心率等于( )
 B.
B. C.
C. D.
D.
 的方程为
的方程为 双曲线
双曲线 的两条渐近线为
的两条渐近线为 和
和 ,过椭圆
,过椭圆 作直线
作直线 ,使得
,使得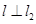 于点
于点 ,又
,又 交于点
交于点 ,
, (如图).
(如图). ,双曲线的焦距为8时,求椭圆的方程;
,双曲线的焦距为8时,求椭圆的方程; ,证明:
,证明: 为常数.
为常数.
 的方程为
的方程为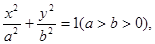 双曲线
双曲线 的两条渐近线为
的两条渐近线为 和
和 ,过椭圆
,过椭圆 作直线
作直线 ,使得
,使得 于点
于点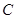 ,又
,又 交于点
交于点 ,
, (如图).
(如图). ,双曲线的焦距为8时,求椭圆的方程;
,双曲线的焦距为8时,求椭圆的方程; ,证明:
,证明: 为常数.
为常数.