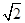题目内容
若直线 与圆C:
与圆C: 相交,则点
相交,则点 的位置是( )
的位置是( )
| A.在圆C外 | B.在圆C内 | C.在圆C上 | D.以上都可能 |
A
解析试题分析:根据直线与圆的位置关系的判定法则,由于直线 与圆C:
与圆C: 相交,可知圆心(0,0),到直线
相交,可知圆心(0,0),到直线 的距离d=
的距离d= ,根据点与圆的位置关系可知点在圆的外面,故选A.
,根据点与圆的位置关系可知点在圆的外面,故选A.
考点:考查了直线与圆的知识。
点评:解决该试题的关键是利用圆心到直线的距离与圆的半径之间的关系来判定,当相交时,则圆心到直线的距离小于圆的半径,属于基础题。

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
若实数x,y满足x²+y²-2x+4y=0,则x-2y的最大值为 ( )
A. | B.10 | C.9 | D.5+2 |
方程 表示圆心为C(2,2),半径为2的圆,则
表示圆心为C(2,2),半径为2的圆,则 的值依次为 ( )
的值依次为 ( )
| A.2、4、4; | B. 、4、4; 、4、4; | C.2、 、4; 、4; | D.2、 、 、 |
直线 与圆
与圆 相交于M、N两点,若
相交于M、N两点,若 ,则k的取值范围为( )
,则k的取值范围为( )
A. | B. | C. | D.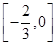 |
圆 和圆
和圆 的位置关系为( )
的位置关系为( )
| A.相交 | B.内切 | C.外切 | D.外离 |
若 ,则直线
,则直线 被圆
被圆 所截得的弦长为( )
所截得的弦长为( )
A. | B.1 | C. | D. |
 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、 ,则称P优于
,则称P优于 ,如果
,如果
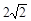 D、8
D、8 与圆
与圆 的两个交点,则
的两个交点,则 ( )
( ) D.
D.