题目内容
6.对于实数集A={x|x2-2ax+(4a-3)=0}和B={x|x2-2$\sqrt{2}$ax+(a2+a+2)=0},是否存在实数a,使A∪B=∅?若a不存在,请说明理由;若a存在,请求出实数a的取值范围.分析 若A∪B=∅,则方程x2-2ax+(4a-3)=0和x2-2$\sqrt{2}$ax+(a2+a+2)=0均为空集,故$\left\{\begin{array}{l}4{a}^{2}-4(4a-3)<0\\ 8{a}^{2}-4({a}^{2}+a+2)<0\end{array}\right.$,解得答案.
解答 解:若A∪B=∅,则方程x2-2ax+(4a-3)=0和x2-2$\sqrt{2}$ax+(a2+a+2)=0均为空集,
故$\left\{\begin{array}{l}4{a}^{2}-4(4a-3)<0\\ 8{a}^{2}-4({a}^{2}+a+2)<0\end{array}\right.$,
解得:a∈(1,2)
点评 本题考查的知识是集合的并集运算,方程根的个数与判断式的关系,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
7.设x3=8,则f(x)=(x-1)(x+1)(x2+x+1)的值是( )
| A. | 7 | B. | 15 | C. | 35 | D. | 21 |
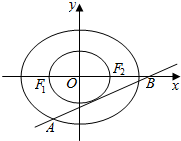 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{3}$),离心率为$\frac{1}{2}$,左右焦点分别为F1(-c,0),F2(c,0).
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{3}$),离心率为$\frac{1}{2}$,左右焦点分别为F1(-c,0),F2(c,0).