题目内容
 如图,圆心角∠AOB=120°,P是
如图,圆心角∠AOB=120°,P是  | AB |
分析:根据题意,由圆周角定理,可得∠AEB=60°,根据圆内接四边形对角互补知,∠BPA=180°-∠AEB=180°-∠BPC,从而∠BPC=∠AEB.即可求得∠BPC.
解答:解 :设点E是优弧AB(不与A、B重合)上的一点,
:设点E是优弧AB(不与A、B重合)上的一点,
∵∠AOB=120°,
∴∠AEB=60°,
∵∠BPA=180°-∠AEB=180°-∠BPC,
∴∠BPC=∠AEB.
∴∠BPC=60°.
故答案为60°.
 :设点E是优弧AB(不与A、B重合)上的一点,
:设点E是优弧AB(不与A、B重合)上的一点,∵∠AOB=120°,
∴∠AEB=60°,
∵∠BPA=180°-∠AEB=180°-∠BPC,
∴∠BPC=∠AEB.
∴∠BPC=60°.
故答案为60°.
点评:本题考查了圆周角定理,在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.和圆内接四边形对角互补的知识.

练习册系列答案
相关题目
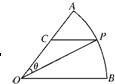 如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.
如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值. 如图,扇形AOB的圆心角为60°,半径为6cm,C,D分别是
如图,扇形AOB的圆心角为60°,半径为6cm,C,D分别是 如图,圆心角∠AOB=120°,P是
如图,圆心角∠AOB=120°,P是  上任一点(不与A,B重合),点C在AP的延长线上,则∠BPC等于 ________.
上任一点(不与A,B重合),点C在AP的延长线上,则∠BPC等于 ________. 上任一点(不与A,B重合),点C在AP的延长线上,则∠BPC等于 .
上任一点(不与A,B重合),点C在AP的延长线上,则∠BPC等于 .