题目内容
若数列{xn}满足xn-xn-1=d(n∈N*,n≥2,其中d为常数),x1+x2+…+x20=80,则x5+x16=________.
8
分析:根据数列{xn}满足xn-xn-1=d,得到此数列为等差数列,由x1+x2+…+x20=80,利用等差数列的前n项和公式表示出前20项的和等于80,根据等差数列的性质可知项数之和相等的两项之和相等,得到10(x5+x16)等于80,即可求出x5+x16的值.
解答:根据题意可知数列{xn}为等差数列,
则x1+x2+…+x20=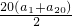 =10(a1+a20)=10(x5+x16)=80,
=10(a1+a20)=10(x5+x16)=80,
所以x5+x16=8.
故答案为:8
点评:此题考查学生掌握数列为等差数列的确定方法,灵活运用等差数列的性质化简求值,是一道基础题.
分析:根据数列{xn}满足xn-xn-1=d,得到此数列为等差数列,由x1+x2+…+x20=80,利用等差数列的前n项和公式表示出前20项的和等于80,根据等差数列的性质可知项数之和相等的两项之和相等,得到10(x5+x16)等于80,即可求出x5+x16的值.
解答:根据题意可知数列{xn}为等差数列,
则x1+x2+…+x20=
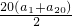 =10(a1+a20)=10(x5+x16)=80,
=10(a1+a20)=10(x5+x16)=80,所以x5+x16=8.
故答案为:8
点评:此题考查学生掌握数列为等差数列的确定方法,灵活运用等差数列的性质化简求值,是一道基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目