题目内容
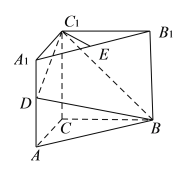
【题目】(本小题满分14分)一种画椭圆的工具如图1所示.![]() 是滑槽
是滑槽![]() 的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且
的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且![]() ,
,![]() .当栓子D在滑槽AB内作往复运动时,带动N绕
.当栓子D在滑槽AB内作往复运动时,带动N绕![]() 转动,M处的笔尖画出的椭圆记为C.以
转动,M处的笔尖画出的椭圆记为C.以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.
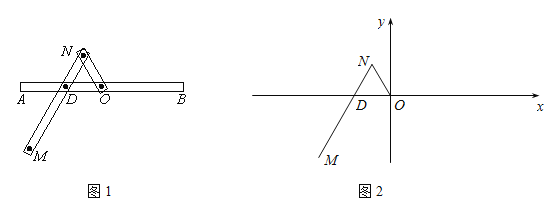
(Ⅰ)求椭圆C的方程;
(Ⅱ)设动直线![]() 与两定直线
与两定直线![]() 和
和![]() 分别交于
分别交于![]() 两点.若直线
两点.若直线![]() 总与椭圆
总与椭圆![]() 有且只有一个公共点,试探究:
有且只有一个公共点,试探究:![]() 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
【答案】(Ⅰ)![]() (Ⅱ)当直线
(Ⅱ)当直线![]() 与椭圆
与椭圆![]() 在四个顶点处相切时,
在四个顶点处相切时,![]() 的面积取得最小值8.
的面积取得最小值8.
【解析】
(Ⅰ)因为![]() ,当
,当![]() 在x轴上时,等号成立;同理
在x轴上时,等号成立;同理![]() ,当
,当![]() 重合,即
重合,即![]() 轴时,等号成立. 所以椭圆C的中心为原点
轴时,等号成立. 所以椭圆C的中心为原点![]() ,长半轴长为
,长半轴长为![]() ,短半轴长为
,短半轴长为![]() ,其方程为
,其方程为![]()
(Ⅱ)(1)当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 为
为![]() 或
或![]() ,都有
,都有![]() .
.
(2)当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() , 由
, 由![]() 消去
消去![]() ,可得
,可得![]() .因为直线
.因为直线![]() 总与椭圆
总与椭圆![]() 有且只有一个公共点,所以
有且只有一个公共点,所以![]() ,即
,即![]() . ①
. ①
又由![]() 可得
可得![]() ;同理可得
;同理可得![]() .由原点
.由原点![]() 到直线
到直线![]() 的距离为
的距离为![]() 和
和![]() ,可得
,可得
![]() . ②
. ②
将①代入②得,![]() . 当
. 当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .因
.因![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 时取等号.所以当
时取等号.所以当![]() 时,
时,![]() 的最小值为8.
的最小值为8.
综合(1)(2)可知,当直线![]() 与椭圆
与椭圆![]() 在四个顶点处相切时,
在四个顶点处相切时,![]() 的面积取得最小值8.
的面积取得最小值8.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案【题目】某工厂每年定期对职工进行培训以提高工人的生产能力(生产能力是指一天加工的零件数).现有![]() 、
、![]() 两类培训,为了比较哪类培训更有利于提高工人的生产能力,工厂决定从同一车间随机抽取100名工人平均分成两个小组分别参加这两类培训.培训后测试各组工人的生产能力得到如下频率分布直方图.
两类培训,为了比较哪类培训更有利于提高工人的生产能力,工厂决定从同一车间随机抽取100名工人平均分成两个小组分别参加这两类培训.培训后测试各组工人的生产能力得到如下频率分布直方图.
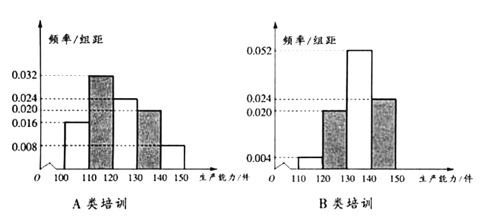
(1)记![]() 表示事件“参加
表示事件“参加![]() 类培训工人的生产能力不低于130件”,估计事件
类培训工人的生产能力不低于130件”,估计事件![]() 的概率;
的概率;
(2)填写下面列联表,并根据列联表判断是否有![]() 的把握认为工人的生产能力与培训类有关:
的把握认为工人的生产能力与培训类有关:
生产能力 | 生产能力 | 总计 | |
| 50 | ||
| 50 | ||
总计 | 100 |
(3)根据频率分布直方图,判断哪类培训更有利于提高工人的生产能力,请说明理由.
参考数据
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式:![]() ,其中
,其中![]() .
.
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.