题目内容
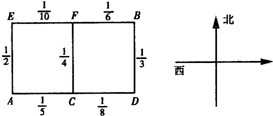 某人居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为
某人居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为| 1 |
| 5 |
| 1 |
| 8 |
(1)请你为其选择一条由A到B的最短路线(即此人只选择从西向东和从南向北的路线),使得途中发生堵车事件的概率最小;
(2)若记路线A→C→F→B中遇到堵车次数为随机变量ξ,求ξ的数学期望Eξ.
分析:(1)各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,利用相互独立事件的概率公式做出各个路段堵车的概率,得到选择路线A→C→F→B,可使得途中发生堵车事件的概率最小.
(2)由题意知路线A→C→F→B中遇到堵车次数ξ可取值为0,1,2,3,结合变量对应的事件和相互独立事件的概率公式,写出变量对应的概率,做出期望值.
(2)由题意知路线A→C→F→B中遇到堵车次数ξ可取值为0,1,2,3,结合变量对应的事件和相互独立事件的概率公式,写出变量对应的概率,做出期望值.
解答:解:(1)记路段MN发生堵车事件为MN.
∵各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,
∴路线A→C→D→B中遇到堵车的概率P1为
1-P(
•
•
)=1-P(
)•P(
)•P(
)
=1-[1-P(AC)][1-P(CD)][1-P(DB)]=1-
•
•
=
;(3分)
同理:路线A→C→F→B中遇到堵车的概率P2为1-P(
•
•
)=
(小于
)
路线A→E→F→B中遇到堵车的概率P3为1-P(
•
•
)=
(大于
)
显然要使得由A到B的路线途中发生堵车事件的概率最小,只可能在以上三条路线中选择.
因此选择路线A→C→F→B,可使得途中发生堵车事件的概率最小
(2)路线A→C→F→B中遇到堵车次数ξ可取值为0,1,2,3.
P(ξ=0)=P(
•
•
)=
P(ξ=1)=P(AC•
•
)+P(
•CF•
)+P(
•
•
)
=
•
•
+
•
•
+
•
•
=
P(ξ=2)=P(AC•CF•
)+P(AC•
•FB)+P(
•CF•FB)
=
•
•
+
•
•
+
•
•
=
P(ξ=3)=P(AC•CF•FB)=
•
•
=
,
∴Eξ=0×
+1×
+2×
+3×
=
答:路线A→C→F→B中遇到堵车次数的数学期望为
.
∵各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,
∴路线A→C→D→B中遇到堵车的概率P1为
1-P(
. |
| AC |
. |
| CD |
. |
| DB |
. |
| AC |
. |
| CD |
. |
| DB |
=1-[1-P(AC)][1-P(CD)][1-P(DB)]=1-
| 4 |
| 5 |
| 7 |
| 8 |
| 2 |
| 3 |
| 8 |
| 15 |
同理:路线A→C→F→B中遇到堵车的概率P2为1-P(
. |
| AC |
. |
| CF |
. |
| FB |
| 1 |
| 2 |
| 8 |
| 15 |
路线A→E→F→B中遇到堵车的概率P3为1-P(
. |
| AE |
. |
| EF |
. |
| FB |
| 5 |
| 8 |
| 8 |
| 15 |
显然要使得由A到B的路线途中发生堵车事件的概率最小,只可能在以上三条路线中选择.
因此选择路线A→C→F→B,可使得途中发生堵车事件的概率最小
(2)路线A→C→F→B中遇到堵车次数ξ可取值为0,1,2,3.
P(ξ=0)=P(
. |
| AC |
. |
| CF |
. |
| FB |
| 1 |
| 2 |
P(ξ=1)=P(AC•
. |
| CF |
. |
| FB |
. |
| AC |
. |
| FB |
. |
| AC |
. |
| CF |
. |
| FB |
=
| 1 |
| 5 |
| 3 |
| 4 |
| 5 |
| 6 |
| 4 |
| 5 |
| 1 |
| 4 |
| 5 |
| 6 |
| 4 |
| 5 |
| 3 |
| 4 |
| 1 |
| 6 |
| 47 |
| 120 |
P(ξ=2)=P(AC•CF•
. |
| FB |
. |
| CF |
. |
| AC |
=
| 1 |
| 5 |
| 1 |
| 4 |
| 5 |
| 6 |
| 1 |
| 5 |
| 3 |
| 4 |
| 1 |
| 6 |
| 4 |
| 5 |
| 1 |
| 4 |
| 1 |
| 6 |
| 12 |
| 120 |
P(ξ=3)=P(AC•CF•FB)=
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 120 |
∴Eξ=0×
| 1 |
| 2 |
| 47 |
| 120 |
| 12 |
| 120 |
| 1 |
| 120 |
| 37 |
| 60 |
答:路线A→C→F→B中遇到堵车次数的数学期望为
| 37 |
| 60 |
点评:本题考查离散型随机变量的期望和相互独立事件的概率,本题是一个易错题,易错点在题目中出现的道路情况比较多,需要仔细写出不要出错.

练习册系列答案
相关题目
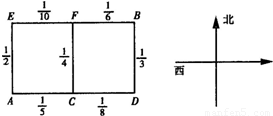
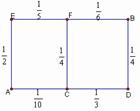 某人居住在城镇的A处,准备开车到单位上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车时间的概率如右图(例如算两个路段:路段发生堵车事件的概率为,路段发生堵车事件的概率为).请你为其选择一条由至的线路,使途中发生堵车的概率最小.
某人居住在城镇的A处,准备开车到单位上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车时间的概率如右图(例如算两个路段:路段发生堵车事件的概率为,路段发生堵车事件的概率为).请你为其选择一条由至的线路,使途中发生堵车的概率最小.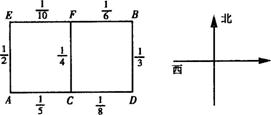
 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为 )
)
 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为 )
)