题目内容
已知离散型随机变量的概率分布如下:
|
分析:由离散型随机变量ξ的概率分布列,先求出k,然后利用数学期望的计算公式求出Eξ,再由离散型随机变量的数学期望的性质,求出随机变量η=2ξ+1的数学期望.
解答:解:由题设知:0.3+3k+4k=1,
∴k=0.1,
∴Eξ=0×0.3+1×0.3+2×0.4=1.1,
∵η=2ξ+1,
∴E(2ξ+1)=2Eξ+1=2.2+1=3.2.
故选B.
∴k=0.1,
∴Eξ=0×0.3+1×0.3+2×0.4=1.1,
∵η=2ξ+1,
∴E(2ξ+1)=2Eξ+1=2.2+1=3.2.
故选B.
点评:本题考查离散型随机变量的数学期望,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
已知离散型随机变量ξ的分布列为:
且ξ的数学期望E(ξ)=
,则
(
)dx=( )
| ξ | a | 2a | 3a |
| P | b | 2b | 2b |
| 11 |
| 5 |
| ∫ | 10b a |
| 1 |
| x |
| A、1+ln2 | B、1 |
| C、-1+ln2 | D、ln2 |
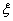 的分布列如图,设
的分布列如图,设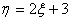 ,则( )
,则( )


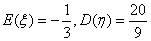 B、
B、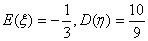
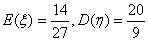 D、
D、