题目内容

已知函数．
（1）求f（f（2））的值；
（2）判断函数在（﹣1，+∞）上单调性，并用定义加以证明．

解：（1）∵函数．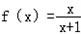
∴f（2）=
∴f（f（2））=f（）=
（2）函数在（﹣1，+∞）上单调递增，理由如下：
任取区间（﹣1，+∞）上两个实数x1，x2，
且x1＜x2，则x1﹣x2＜0，x1+1＞，x2+1＞0
则f（x1）﹣f（x2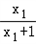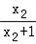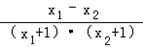）=﹣=＜0
即f（x1）＜f（x2）
故函数在（﹣1，+∞）上为增函数

练习册系列答案
相关题目
已知函数．
（1）求f（x）的最大值及取得最大值时的x集合；
（2）设△ABC的角A，B，C的对边分别为a，b，c，且a=1，f（A）=0．求b+c的取值范围．
已知函数．
（1）求f（f（3））的值；
（2）判断函数在（1，+∞）上单调性，并用定义加以证明．
（3）当x取什么值时，的图象在x轴上方？
已知函数．
（1）求f（x）的最小正周期和值域；
（2）若x=x为f（x）的一个零点，求sin2x的值．
已知函数．
（1）求f（x）的最小正周期；
（2）求f（x）的单调递减区间；
（3）函数f（x）的图象经过怎样的平移才能使其对应的函数成为奇函数？
已知函数．
（1）求f（x）的最小正周期及对称中心；
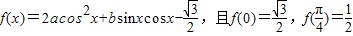（2）若，求f（x）的最大值和最小值．