题目内容
已知幂函数y=f(x)的图象经过点 .
.
(1)求函数f(x)的解析式,并写出f(x)的定义域;
(2)判断函数f(x)的单调性,并证明你的结论.
解:(1)依题意设y=xα,
∵函数y=f(x)的图象经过点 ,
,
∴ ,∴
,∴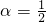 ,∴
,∴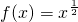 ,
,
由 可知:f(x)的定义域为[0,+∞)
可知:f(x)的定义域为[0,+∞)
(2)函数f(x)在[0,+∞)上是增函数;
证明:任取x1,x2∈[0,+∞),且x1<x2,
则
= ,
,
∵x1-x2<0,
∴f(x1)<f(x2)
所以函数 在[0,+∞)上是增函数.
在[0,+∞)上是增函数.
分析:(1)利用幂函数的形式设出其方程,将点的坐标代入求出解析式.
(2)利用函数单调性的定义证明函数的单调性.关键是将函数值的差变形.
点评:本题考查利用待定系数法求模型已知的函数的解析式;利用函数单调性的定义证明函数的单调性.
∵函数y=f(x)的图象经过点
 ,
,∴
 ,∴
,∴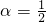 ,∴
,∴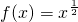 ,
,由
 可知:f(x)的定义域为[0,+∞)
可知:f(x)的定义域为[0,+∞)(2)函数f(x)在[0,+∞)上是增函数;
证明:任取x1,x2∈[0,+∞),且x1<x2,
则

=
 ,
,∵x1-x2<0,

∴f(x1)<f(x2)
所以函数
 在[0,+∞)上是增函数.
在[0,+∞)上是增函数.分析:(1)利用幂函数的形式设出其方程,将点的坐标代入求出解析式.
(2)利用函数单调性的定义证明函数的单调性.关键是将函数值的差变形.
点评:本题考查利用待定系数法求模型已知的函数的解析式;利用函数单调性的定义证明函数的单调性.

练习册系列答案
相关题目